
【题目】新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
【答案】解:算法:
第一步:输入考试成绩C1和平时成绩C2 ,
第二步:计算模块成绩c=![]()
第三步:判断C与60的大小,输出学分F
若C≥60,则输出F=2;
若C<60,则输出F=0.
程序框图:(如图)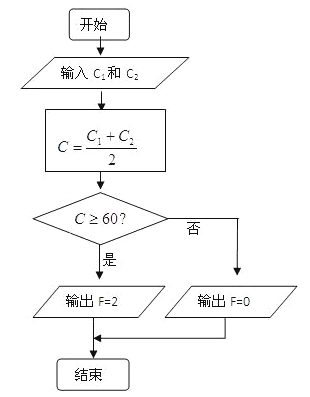
【解析】首先根据是解题所给的条件,模块成绩大于或等于60分,获得2学分,否则不能获得学分,根据条件设计一个算法,判断C与60的大小,输出学分F,关键是若C≥60,则输出F=2;若C<60,则输出F=0,进而根据做出的算法,画出程序框图,注意条件的设置.
【考点精析】解答此题的关键在于理解算法的条件结构的相关知识,掌握条件P是否成立而选择执行A框或B框.无论P条件是否成立,只能执行A框或B框之一,不可能同时执行A框和B框,也不可能A框、B框都不执行.一个判断结构可以有多个判断框.


科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液.已知每投放a(1≤a≤4且a∈R)个单位的营养液,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=af(x),其中f(x)= 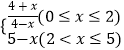 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次4个单位的营养液,则有效时间可能达几天?
(2)若先投放2个单位的营养液,3天后投放b个单位的营养液.要使接下来的2天中,营养液能够持续有效,试求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电耗如表:
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点. 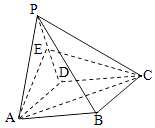
(1)求证:PB⊥AC.
(2)求二面角E﹣AC﹣D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题甲:关于x的不等式x2+(a﹣1)x+a2>0的解集为R;命题乙:函数y=(2a2﹣a)x为增函数,当甲、乙有且只有一个是真命题时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣2,2]
C.[﹣1,1]
D.[﹣4,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= ![]() AB=1,M为PB中点.
AB=1,M为PB中点. 
(1)证明:CM∥平面PAD;
(2)求二面角A﹣MC﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com