
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
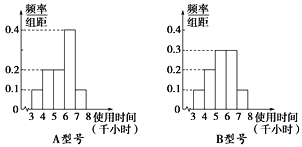
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.
科目:高中数学 来源: 题型:
【题目】盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机取出2个球,求取出的2个球的颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x1,x2,x3,随机变量X表示x1,x2,x3中的最大数,求X的概率分布和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.函数
轴平行.函数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:函数![]() 共有两个零点,一个零点是
共有两个零点,一个零点是![]() ,另一个零点
,另一个零点![]() 在区间
在区间![]() 内;
内;
(Ⅲ)求证:存在![]() ,当
,当![]() 时,
时, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 过坐标原点
过坐标原点![]() 且圆心在曲线
且圆心在曲线![]() 上.
上.
(1)求圆![]() 面积的最小值;
面积的最小值;
(2)设直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求圆
,求圆![]() 的方程;
的方程;
(3)设直线![]() 与(2)中所求圆
与(2)中所求圆![]() 交于点
交于点![]() 、
、![]() ,
,![]() 为直线
为直线![]() 上的动点,直线
上的动点,直线![]() ,
,![]() 与圆
与圆![]() 的另一个交点分别为
的另一个交点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
:  (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
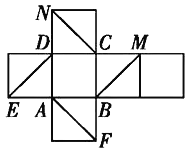
【题目】如图所示是一个正方体的平面展开图,在这个正方体中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四个命题中,真命题的序号是
平面NCF.以上四个命题中,真命题的序号是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com