
【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形. 
(1)证明:PB⊥CD;
(2)求二面角A﹣PD﹣C的大小.
【答案】
(1)证明:取BC的中点E,连接DE,可得四边形ABED是正方形
过点P作PO⊥平面ABCD,垂足为O,连接OA、OB、OD、OE
∵△PAB与△PAD都是等边三角形,∴PA=PB=PD,可得OA=OB=OD
因此,O是正方形ABED的对角线的交点,可得OE⊥OB
∵PO⊥平面ABCD,得直线OB是直线PB在内的射影,∴OE⊥PB
∵△BCD中,E、O分别为BC、BD的中点,∴OE∥CD,可得PB⊥CD;
(2)解:由(1)知CD⊥PO,CD⊥PB
∵PO、PB是平面PBD内的相交直线,∴CD⊥平面PBD
∵PD平面PBD,∴CD⊥PD
取PD的中点F,PC的中点G,连接FG,
则FG为△PCD有中位线,∴FG∥CD,可得FG⊥PD
连接AF,由△PAD是等边三角形可得AF⊥PD,∴∠AFG为二面角A﹣PD﹣C的平面角
连接AG、EG,则EG∥PB
∵PB⊥OE,∴EG⊥OE,
设AB=2,则AE=2 ![]() ,EG=
,EG= ![]() PB=1,故AG=
PB=1,故AG= ![]() =3
=3
在△AFG中,FG= ![]() CD=
CD= ![]() ,AF=
,AF= ![]() ,AG=3
,AG=3
∴cos∠AFG= ![]() =﹣
=﹣ ![]() ,得∠AFG=π﹣arccos
,得∠AFG=π﹣arccos ![]() ,
,
即二面角A﹣PD﹣C的平面角大小是π﹣arccos ![]() .
.
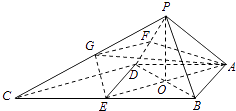
【解析】(1)取BC的中点E,连接DE,过点P作PO⊥平面ABCD于O,连接OA、OB、OD、OE.可证出四边形ABED是正方形,且O为正方形ABED的中心.因此OE⊥OB,结合三垂线定理,证出OE⊥PB,而OE是△BCD的中位线,可得OE∥CD,因此PB⊥CD;(2)由(1)的结论,证出CD⊥平面PBD,从而得到CD⊥PD.取PD的中点F,PC的中点G,连接FG,可得FG∥CD,所以FG⊥PD.连接AF,可得AF⊥PD,因此∠AFG为二面角A﹣PD﹣C的平面角,连接AG、EG,则EG∥PB,可得EG⊥OE.设AB=2,可求出AE、EG、AG、AF和FG的长,最后在△AFG中利用余弦定理,算出∠AFG=π﹣arccos ![]() ,即得二面角A﹣PD﹣C的平面角大小.
,即得二面角A﹣PD﹣C的平面角大小.
【考点精析】本题主要考查了直线与平面垂直的性质和共线向量与共面向量的相关知识点,需要掌握垂直于同一个平面的两条直线平行;向量共线的充要条件:对于空间任意两个向量![]() ,
,![]() ,
,![]() 的充要条件是存在实数
的充要条件是存在实数![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年投入固定成本![]() 万元.此外,每生产
万元.此外,每生产![]() 件这种产品还需要增加投入
件这种产品还需要增加投入![]() 万元.经测算,市场对该产品的年需求量为
万元.经测算,市场对该产品的年需求量为![]() 件,且当出售的这种产品的数量为
件,且当出售的这种产品的数量为![]() (单位:百件)时,销售所得的收入约为
(单位:百件)时,销售所得的收入约为![]() (万元).
(万元).
(1)若该公司这种产品的年产量为![]() (单位:百件),试把该公司生产并销售这种产品所得的年利润
(单位:百件),试把该公司生产并销售这种产品所得的年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)当该公司的年产量![]() 为多少时,当年所得利润
为多少时,当年所得利润![]() 最大?最大为多少?
最大?最大为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为促进农业发展,加快农村建设,某地政府扶持兴建了一批“超级蔬菜大棚”,为了解大棚的面积与年利润之间的关系,随机抽取了其中的7个大棚,并对当年的利润进行统计整理后得到了如下数据对比表:

由所给数据的散点图可以看出,各样本点都分布在一条直线附近,并且![]() 与
与![]() 有很强的线性相关关系.
有很强的线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留三位小数);
的线性回归方程;(结果保留三位小数);
(2)小明家的“超级蔬菜大棚”面积为8.0亩,估计小明家的大棚当年的利润为多少;
(3)另外调查了近5年的不同蔬菜亩平均利润(单位:万元),其中无丝豆为:1.5,1.7,2.1,2.2,2.5;彩椒为:1.8,1.9,1.9,2.2,2.2,请分析种植哪种蔬菜比较好?
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.y=f(x)的图象关于(π,0)中心对称
B.y=f(x)的图象关于x= ![]() 对称
对称
C.f(x)的最大值为 ![]()
D.f(x)既是奇函数,又是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学100位学生在市统考中的理科综合分数,以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在![]() 的学生中应抽取多少人?
的学生中应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是含数1的有限实数集,f(x)是定义在D上的函数。若f(x)的图像绕原点逆时针旋转![]() 后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 0
D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面积.
,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com