
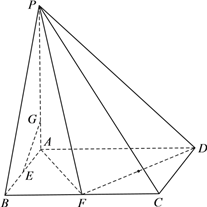
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)PA![]() 面ABCD,
面ABCD, ![]() 面ABCD,
面ABCD, ![]() PA
PA![]() DF ,在矩形内根据F是线段BC的中点和长度,根据勾股定理求得AF
DF ,在矩形内根据F是线段BC的中点和长度,根据勾股定理求得AF![]() DF,即得证 (2)解法一:延长AB交DF延长线于点M,连结PM.这样将面PDF延伸,当EG
DF,即得证 (2)解法一:延长AB交DF延长线于点M,连结PM.这样将面PDF延伸,当EG![]() PM时存在一点G,使得EG
PM时存在一点G,使得EG![]() 面PDF 解法二:构造平行四边形,取DF中点I,连结EI,过点G作AD的平行线交PD于点H,连结GH、HI.证得四边形GEIH是平行四边形,根据线面平行判定定理即可证得。
面PDF 解法二:构造平行四边形,取DF中点I,连结EI,过点G作AD的平行线交PD于点H,连结GH、HI.证得四边形GEIH是平行四边形,根据线面平行判定定理即可证得。
解析:⑴ ![]() PA
PA![]() 面ABCD,
面ABCD, ![]() 面ABCD,
面ABCD, ![]() PA
PA![]() DF,
DF,
又![]() 在底面ABCD中,
在底面ABCD中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() AF
AF![]() DF,
DF,
![]() ,
, ![]() DF
DF![]() 面PAF,
面PAF,
![]() 面PDF,面PAF
面PDF,面PAF![]() 面PDF.
面PDF.
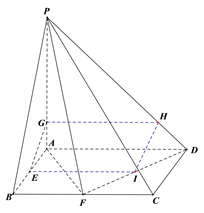
解⑵:法一、假设在线段AP上存在点G,使得EG![]() 面PDF.连结AB并延长交DF延长线于点M,连结PM.
面PDF.连结AB并延长交DF延长线于点M,连结PM.
![]() F是线段BC的中点,底面ABCD是矩形,
F是线段BC的中点,底面ABCD是矩形,
![]() ,
,
![]() EG
EG![]() 面PDM,
面PDM, ![]() 面PAM,面PAM
面PAM,面PAM ![]() 面PDM=PM,
面PDM=PM,
![]() EG
EG![]() PM,
PM,
![]() ,
, ![]() ,
,
故在线段AP上存在点G,使得EG![]() 面PDF,此时
面PDF,此时![]() .
.

法二、假设在线段AP上存在点G,使得EG![]() 面PDF.取DF中点I,连结EI,过点G作AD的平行线交PD于点H,连结GH、HI.
面PDF.取DF中点I,连结EI,过点G作AD的平行线交PD于点H,连结GH、HI.
![]() E是线段AB的中点,
E是线段AB的中点, ![]() 是梯形ABFD的中位线,
是梯形ABFD的中位线,
![]() ,EI
,EI![]() GH,
GH,
![]() EG
EG![]() 面PDF,
面PDF, ![]() 面GEIH,面GEIH
面GEIH,面GEIH ![]() 面PDM=IH,
面PDM=IH,
![]() EG
EG![]() IH,
IH,
![]() 四边形GEIH是平行四边形,
四边形GEIH是平行四边形,
![]() ,
,
![]() ,
, ![]() ,
,
故在线段AP上存在点G,使得EG![]() 面PDF,此时
面PDF,此时![]() .
.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的极值;
的极值;
(Ⅱ)设函数![]() .当
.当![]() 时,若区间
时,若区间![]() 上存在
上存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体户计划经销A、B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A、B商品中所获得的收益分别为f(x)万元与g(x)万元、其中f(x)=a(x﹣1)+2(a>0);g(x)=6ln(x+b),(b>0)已知投资额为零时,收益为零.
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据:ln3≈1.10).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由小到大排列的一组数据x1 , x2 , x3 , x4 , x5 , 其中每个数据都小于﹣1,则样本1,x1 , ﹣x2 , x3 , ﹣x4 , x5的中位数为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0).
(1)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点. 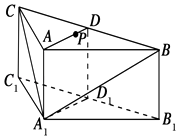
(1)在平面ABC内,试作出过点P与平面A1BC平行的直线l,并说明理由;
(2)证明:直线l⊥平面ADD1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a2x2+ax(a∈R).
(1)当a=1时,求函数f(x)最大值;
(2)若函数f(x)在区间(1,+∞)上是减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com