
 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.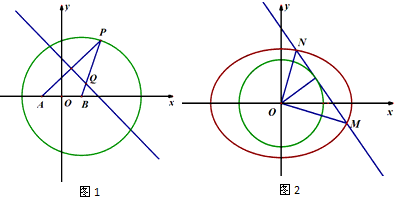
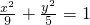 .(5分)
.(5分)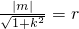 即m2=r2(1+k2)①(7分)
即m2=r2(1+k2)①(7分)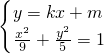 ,消去y得,(5+9k2)x2+18kmx+9(m2-5)=0,
,消去y得,(5+9k2)x2+18kmx+9(m2-5)=0,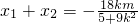 ,
, (9分)
(9分)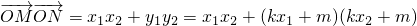 =
=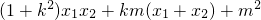
 =
=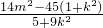 ②(10分)
②(10分) =
=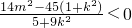
 (12分)
(12分) ,进而
,进而 =
=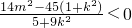
 ,
,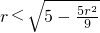 ,得到
,得到 ,同上可得:任意一条切线l均满足∠MON>90°;
,同上可得:任意一条切线l均满足∠MON>90°; ,
,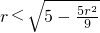 ,对于斜率不存在的切线x=±r也有∠MON>90°.
,对于斜率不存在的切线x=±r也有∠MON>90°.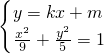 ,消去y,借助于韦达定理,证明
,消去y,借助于韦达定理,证明 =
=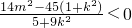 即可,再考虑两种特殊情况:(1)当满足∠MON>90°的那条切线斜率不存在时,切线方程为x=±r,(2)当满足∠MON>90°的那条切线斜率存在时,故结论可证.
即可,再考虑两种特殊情况:(1)当满足∠MON>90°的那条切线斜率不存在时,切线方程为x=±r,(2)当满足∠MON>90°的那条切线斜率存在时,故结论可证.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:
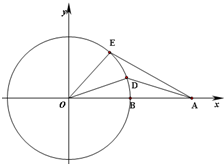 如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π
如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π| π | 6 |
查看答案和解析>>
科目:高中数学 来源:浙江省期中题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年福建省泉州市高三质量检测数学试卷(理科)(解析版) 题型:解答题
 ,求四边形ODAE的面积;
,求四边形ODAE的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com