
【题目】已知![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象
的图象
B. 函数![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. 函数![]() 的图象关于
的图象关于![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内单调递增
内单调递增
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1).
(1)将函数f(x)的图象上的所有点向右平行移动1个单位得到函数g(x)的图象,写出函数g(x)的表达式;
(2)若关于x的函数y=g2(x)﹣mg(x2)+3在[1,4]上的最小值为2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数F(x)=lnx(x>1)的图象与函数G(x)的图象关于直线y=x对称,若函数f(x)=(k﹣1)x﹣G(﹣x)无零点,则实数k的取值范围是( )
A.(1﹣e,1)
B.(1﹣e,∞)
C.(1﹣e,1]
D.(﹣∞,1﹣e)∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .四边形
.四边形![]() 满足
满足![]() ,
,![]() ,
,![]() .
.![]() 为侧棱
为侧棱![]() 的中点,
的中点,![]() 为侧棱
为侧棱![]() 上的任意一点.
上的任意一点.
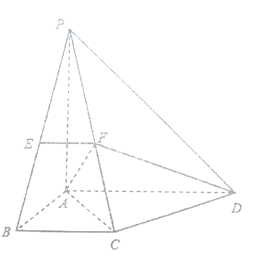
(1)若![]() 为
为![]() 的中点,求证: 面
的中点,求证: 面![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直? 若存在,写出证明过程并求出线段
垂直? 若存在,写出证明过程并求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务,该配送站有8名新手快递员和4名老快递员,但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹,日工资320元;每个老快递员每天可配送300件包裹,日工资520元.
(Ⅰ)求该配送站每天需支付快递员的总工资最小值;
(Ⅱ)该配送站规定:新手快递员某个月被评为“优秀”,则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”,日工资会超过老快递员?
(参考数据: ![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中:
①双曲线 ![]() 与椭圆
与椭圆 ![]() 有相同的焦点;
有相同的焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设A,B为两个定点,k为常数,若|PA|﹣|PB|=k,则动点P的轨迹为双曲线;
④过定圆C上一点A作圆的动弦AB,O为原点,若 ![]() 则动点P的轨迹为椭圆.其中正确的个数是( )
则动点P的轨迹为椭圆.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x+y+2=0,l2:mx+4y+n=0
(1)若l1⊥l2 , 求m的值,;
(2)若l1∥l2 , 且它们的距离为 ![]() ,求m、n的值.
,求m、n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4sinθ.
(1)求曲线C的直角坐标方程;
(2)若曲线C1: ![]() (α为参数)与曲线C所表示的图形都相切,求r的值.
(α为参数)与曲线C所表示的图形都相切,求r的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com