分析:(I)求导函数,令f′(x)>0,解得f(x)的单调增区间;
(II)当x∈(-∞,0)时,h(x)=e
2x-2x是减函数;当x∈[0,+∞)时,h(x)=e
2x-2x是增函数,从而h(x)≥h(0),进而可证对任意
x∈[0,),恒有
1+2x≤e2x≤成立;
(III)当a=0时,得f(x)=e
2x-2x,从而
g(n)=[f(0)+f()+f()+…+f()]=
•-1+,可证
-g(n)≤,根据当
n>时,
<ε,可得当
n>时,不等式
-g(n)<ε总成立
解答:(I)解:f′(x)=2e
x(e
x-a)-2=2(e
2x-ae
x-1)
令f′(x)>0,解得
x>ln∴f(x)的单调增区间是
(ln,+∞)(II)证明:由(I)知,当x∈(-∞,0)时,h(x)=e
2x-2x是减函数;当x∈[0,+∞)时,h(x)=e
2x-2x是增函数;
∴h(x)≥h(0)
∴e
2x-2x≥1
∴e
2x≥2x+1
x∈[0,)时,∴e
-2x≥-2x+1>0
∴
e2x≤∴对任意
x∈[0,),恒有
1+2x≤e2x≤成立;
(III)证明:当a=0时,得f(x)=e
2x-2x
∴
g(n)=[f(0)+f()+f()+…+f()]=
[(1+e+e+…+e)-(++…+)]=
•-1+∵ε∈(0,1),∴当
n>时,
∈(0,)由(II)知,
1<e≤,
0<e-1≤∴
≥-1∴
≥(-1)(e2-1)∴
•≥(-)(e2-1)∴
•-1+≥(-)(e2-1)-1+∴
g(n)≥-∴
-g(n)≤∴当
n>时,
<ε∴当
n>时,不等式
-g(n)<ε总成立
点评:本题以函数为载体,考查导数法求函数的单调区间,考查不等式的证明,解题的关键是充分利用函数的单调性,难度较大.



 名校课堂系列答案
名校课堂系列答案
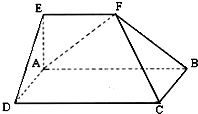 (2010•成都一模)如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
(2010•成都一模)如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.