练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满12分）  已知函数

     （Ⅰ）将函数化简成的形式，并指出的周期；（Ⅱ）求函数上的最大值和最小值

    （Ⅰ）同解析；（2）x=时，f(x)有最小值－；当x=π时，f(x)有最大值－2.


    解析:

    解：(Ⅰ)f(x)=sinx+.

      故f(x)的周期为2kπ｛k∈Z且k≠0｝.

    (Ⅱ)由π≤x≤π，得.

    因为f(x)＝在[]上是减函数，在[]上是增函数.

    故当x=时，f(x)有最小值－；而f(π)=－2，f(π)＝－＜－2，

    所以当x=π时，f(x)有最大值－2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本小题满12分.）已知函数．

    （Ⅰ）当时，若，求函数的值；

    （Ⅱ）当时，求函数的值域；

    （Ⅲ）把函数的图象按向量平移得到函数的图象，若函数是偶函数，写出最小的向量的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满12分.）已知函数．

    （Ⅰ）当时，若，求函数的值；

    （Ⅱ）当时，求函数的值域；

    （Ⅲ）把函数的图象按向量平移得到函数的图象，若函数是偶函数，写出最小的向量的坐标

    查看答案和解析>>

    科目：高中数学 来源：2011届云南省芒市中学高三教学质量检测数学理卷 题型：解答题

    (本小题满分12分）（文科做前两问；理科全做．）
    某会议室用3盏灯照明，每盏灯各使用节能灯棍一只，且型号相同．假定每盏灯能否正常照明只与灯棍的寿命有关，该型号的灯棍寿命为1年以上的概率为0.8，寿命为2年以上的概率为0.3，从使用之日起每满1年进行一次灯棍更换工作，只更换已坏的灯棍，平时不换．
    （I）在第一次灯棍更换工作中，求不需要更换灯棍的概率；
    （II）在第二次灯棍更换工作中，对其中的某一盏灯来说，求该灯需要更换灯棍的概率；
    （III）设在第二次灯棍更换工作中，需要更换的灯棍数为ξ，求ξ的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年黑龙江省高二下学期期中考试理科数学 题型：解答题

    （本小题满分12分）

    甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为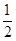，且各局胜负相互独立.求：

    （1）打了两局就停止比赛的概率；

    （2）打满3局比赛还未停止的概率；

    （3）比赛停止时已打局数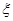的分布列与期望.

     

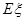    查看答案和解析>>

    同步练习册答案