Question

7．已知在△ABC所在平面内有两点P、Q，满足$\overrightarrow{PA}$+$\overrightarrow{PC}$=0，$\overrightarrow{QA}$+$\overrightarrow{QB}$+$\overrightarrow{QC}$=$\overrightarrow{BC}$，若|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=2，S_△APQ=$\frac{2}{3}$，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为±4$\sqrt{3}$．

Answer 1

分析 由题意可得P为AC的中点，Q为靠近B的线段AB的三等分点，根据S_△APQ=$\frac{2}{3}$，求得sin∠A 的值，可得cos∠A的值，从而求得$\overrightarrow{AB}$•$\overrightarrow{AC}$的值．

解答 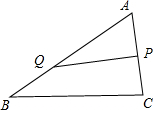解：已知在△ABC所在平面内有点P满足$\overrightarrow{PA}$+$\overrightarrow{PC}$=0，∴P为AC的中点，
∵点Q满足$\overrightarrow{QA}$+$\overrightarrow{QB}$+$\overrightarrow{QC}$=$\overrightarrow{BC}$，即$\overrightarrow{QA}$+$\overrightarrow{QB}$+$\overrightarrow{QC}$=$\overrightarrow{QC}$-$\overrightarrow{QB}$，即$\overrightarrow{QA}$=-2$\overrightarrow{QB}$，
∴Q为靠近B的线段AB的三等分点，如图所示：
若|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=2，则|$\overrightarrow{AP}$|=1，|$\overrightarrow{AQ}$|=$\frac{2}{3}$|$\overrightarrow{AB}$|=$\frac{8}{3}$，
∴S_△APQ=$\frac{1}{2}$•|$\overrightarrow{AP}$|•|$\overrightarrow{AQ}$|•cos∠A=$\frac{1}{2}$•1•$\frac{8}{3}$•sin∠A=$\frac{2}{3}$，
∴sin∠A=$\frac{1}{2}$，∴cos∠A=±$\sqrt{{1-sin}^{2}∠A}$=±$\frac{\sqrt{3}}{2}$，
则$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠A=±4$\sqrt{3}$，
故答案为：±4$\sqrt{3}$．

点评 考查向量减法及数乘的几何意义，向量的数乘运算，三角形的面积公式，向量数量积的计算公式，属于中档题．