
【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
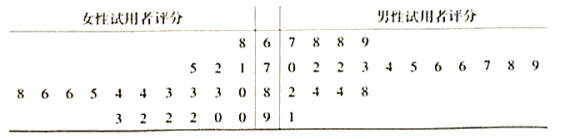
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: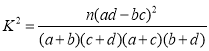 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)![]() ; (2)①
; (2)①![]() ; ②有
; ②有![]() 的把握认为“认定类型”与性别有关.
的把握认为“认定类型”与性别有关.
【解析】
(1)根据茎叶图中的数据,即可容易求得中位数;
(2)①根据样本数据,计算评分不小于81的频率,乘以600,即为所求;
②根据题意,补全列联表,计算![]() ,据此判断.
,据此判断.
(1)由茎叶图中数据可知,中间两个数分别为![]() ,
,
故中位数![]() ;
;
(2)因为![]() ,所以
,所以![]() ;
;
①由茎叶图知,女性试用者评分不小于81的有15个,
男性试用者评分不小于81的有5个,
所以在40个样本数据中,评分不小于81的频率为![]() .
.
可以估计收回的600份评分表中,评分不小于81的份数为![]() ;
;
②根据题意得2×2列联表:
满意型 | 需改进型 | 合计 | |
女性 | 15 | 5 | 20 |
男性 | 5 | 15 | 20 |
合计 | 20 | 20 | 40 |
由于![]() ,
,
查表得![]() ,
,
所以有![]() 的把握认为“认定类型”与性别有关.
的把握认为“认定类型”与性别有关.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
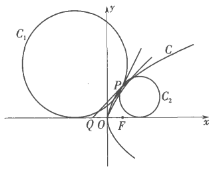
【题目】如图,在平面直角坐标系xOy中,F为x轴正半轴上的一个动点.以F为焦点、O为顶点作抛物线C.设P为第一象限内抛物线C上的一点,Q为x轴负半轴上一点,使得PQ为抛物线C的切线,且![]() .圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
.圆C1、C2均与直线OP切于点P,且均与x轴相切.求点F的坐标,使圆C1与C2的面积之和取到最小值,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:
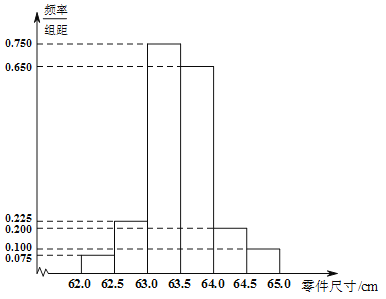
注:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(Ⅰ) 从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅱ) 从产品中随机抽取![]() 件,全是合格品的概率不小于
件,全是合格品的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ) 为了提高产品合格率,现提出![]() 两种不同的改进方案进行试验.若按
两种不同的改进方案进行试验.若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ;若按
;若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设函数![]() 的定义域为
的定义域为![]() ,且有极值点.
,且有极值点.
(ⅰ) 试判断当![]() 时,
时, ![]() 是否满足题目的条件,并说明理由;
是否满足题目的条件,并说明理由;
(ⅱ) 设函数![]() 的极小值点为
的极小值点为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要考察某公司生产的![]() 克袋装牛奶的质量是否达标,现从
克袋装牛奶的质量是否达标,现从![]() 袋牛奶中抽取
袋牛奶中抽取![]() 袋牛奶进行检验,利用随机数表抽样时,先将
袋牛奶进行检验,利用随机数表抽样时,先将![]() 袋牛奶按
袋牛奶按![]() 、
、![]() 、
、![]() 、
、![]() 进行编号,如果从随机数表第
进行编号,如果从随机数表第![]() 行第
行第![]() 列开始向右读,请你依次写出最先检测的
列开始向右读,请你依次写出最先检测的![]() 袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第
袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第![]() 行至第
行至第![]() 行)
行)
8842 1753 3157 2455 0688 7704 7476 7217 6335 0258 3921 2067 64
6301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 79
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,且与
,且与![]() 轴有唯一的交点
轴有唯一的交点![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,记此函数的最小值为
,记此函数的最小值为![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com