
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系![]() 的极坐标方程为
的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() ,(其中
,(其中![]() 为参数)直线l与
为参数)直线l与![]() 交于A,B两个不同的点.
交于A,B两个不同的点.
![]() 求倾斜角
求倾斜角![]() 的取值范围;
的取值范围;
![]() 求线段AB中点P的轨迹的参数方程.
求线段AB中点P的轨迹的参数方程.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() 是参数).
是参数).
【解析】
(1)直接利用转换关系,把参数方程直角坐标方程和极坐标方程之间进行转换![]() 进一步利用点到直线的距离公式的应用求出
进一步利用点到直线的距离公式的应用求出![]() 的取值范围.
的取值范围.
(2)进一步利用直线和曲线的位置关系和一元二次方程根和系数关系和中点的坐标公式的应用求出结果.
(1)直线![]() 的倾斜角为
的倾斜角为![]() ,
,
当![]() 时,直线
时,直线![]() (即
(即![]() 轴)与
轴)与![]() 交于
交于![]() 两个不同的点,符合题目要求;
两个不同的点,符合题目要求;
当![]() 时,记
时,记![]() ,
,
直线![]() 的参数方程为
的参数方程为![]() 化为普通方程得
化为普通方程得![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() .
.
直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,
解得:![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的倾斜角
的倾斜角![]() 的取值范围是
的取值范围是![]() ;
;
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,
,
综上,直线![]() 的倾斜角
的倾斜角![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() 的极坐标方程为
的极坐标方程为![]() ,其直角坐标方程为
,其直角坐标方程为![]() ,
,
因直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数
为参数![]() ,
,
故可设![]() ,
,![]() ,
,
代入![]() 中得到:
中得到:![]() ,
,
注意到![]() ,
,![]() 为方程的根,故
为方程的根,故![]() ,
,
点![]() 的坐标为
的坐标为![]() 即
即![]() ,
,
所以点![]() 的轨迹参数方程为:
的轨迹参数方程为:![]() (
(![]() 为参数).
为参数).


科目:高中数学 来源: 题型:
【题目】已知四边形ABCD外切于![]() ,△ACB的内切圆
,△ACB的内切圆![]() 与边AB、BC的切点分别为P、Q,,△ACD的内切圆
与边AB、BC的切点分别为P、Q,,△ACD的内切圆![]() 与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为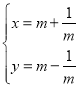 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我市举行“四川省运动会”期间,组委会将甲、乙、丙、丁四位志愿者全部分配到![]() 三个运动场馆执勤.若每个场馆至少分配一人,则不同分配方案的种数是( )
三个运动场馆执勤.若每个场馆至少分配一人,则不同分配方案的种数是( )
A. 24B. 36C. 72D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:
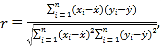
![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,三个点
,三个点![]() ,
, ![]() ,
, ![]() 中恰有两个点在
中恰有两个点在![]() 上.
上.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线交
的直线交![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 为
为![]() 上任意一点,证明:直线
上任意一点,证明:直线![]() ,
, ![]() ,
, ![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
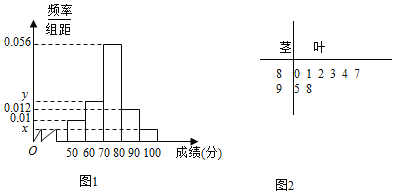
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com