
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上具有单调性,求实数
上具有单调性,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若在区间![]() 上,函数
上,函数![]() 的图象恒在
的图象恒在![]() 图象上方,求实数
图象上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)求出函数的对称轴,根据二次函数的单调性求出实数![]() 的取值范围;(2)问题转化为
的取值范围;(2)问题转化为![]() (m+1)x+m+2>0对任意x∈[1,1]恒成立,设h(x)=x2(m+1)x+m+2,通过讨论对称轴的范围,求出实数
(m+1)x+m+2>0对任意x∈[1,1]恒成立,设h(x)=x2(m+1)x+m+2,通过讨论对称轴的范围,求出实数![]() 的取值范围.
的取值范围.
试题解析:
(1)对称轴x=![]() ,且图象开口向上。
,且图象开口向上。
若函数g(x)在[2,4]上具有单调性,
则满足![]() 2或
2或![]() 4,
4,
解得:m5或m9;
(2)若在区间[1,1]上,函数y=g(x)的图象恒在y=2x9图象上方,
则只需:![]() >2x9在区间[1,1]恒成立,
>2x9在区间[1,1]恒成立,
即![]() (m+1)x+m+2>0对任意x∈[1,1]恒成立,
(m+1)x+m+2>0对任意x∈[1,1]恒成立,
设h(x)=x2(m+1)x+m+2其图象的对称轴为直线x=![]() ,且图象开口向上
,且图象开口向上
①当![]() 1即m1时,h(x)在[1,1]上是减函数,
1即m1时,h(x)在[1,1]上是减函数,
所以h(x)min=h(1)=2>0,
所以:m1;
②当1<![]() <1,即3<m<1,函数h(x)在顶点处取得最小值,
<1,即3<m<1,函数h(x)在顶点处取得最小值,
即h(x)min=h(![]() )=m+2
)=m+2![]() >0,解得:
>0,解得:![]() <m<1;
<m<1;
③当![]() 1即m3时,h(x)在[1,1]上是增函数,
1即m3时,h(x)在[1,1]上是增函数,
所以,h(x)min=h(1)=2m+4>0,解得:m&g;2,
此时,m∈;
综上所述:![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足 ![]() =λ
=λ ![]() .
. 
(1)若λ= ![]() ,用向量
,用向量 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(2)若| ![]() |=4,|
|=4,| ![]() |=3,且∠AOB=60°,求
|=3,且∠AOB=60°,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=ax+1﹣a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y=﹣2|x﹣1|;②y=x2;③(x﹣1)2+(y﹣1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有( )
A.①④
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ) 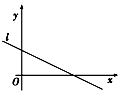
A.已知购买一张彩票中奖的概率为 ![]() ,则购买1000张这种彩票一定能中奖
,则购买1000张这种彩票一定能中奖
B.互斥事件一定是对立事件
C.如图,直线l是变量x和y的线性回归方程,则变量x和y相关系数在﹣1到0之间
D.若样本x1 , x2 , …xn的方差是4,则x1﹣1,x2﹣1,…xn﹣1的方差是3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |

(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生态公园的平面图呈长方形(如图),已知生态公园的长AB=8(km),宽AD=4(km),M,N分别为长方形ABCD边AD,DC的中点,P,Q为长方形ABCD边AB,BC(不含端点)上的一点.现公园管理处拟修建观光车道P﹣Q﹣N﹣M﹣P,要求观光车道围成四边形(如图阴影部分)的面积为15(km2),设BP=x(km),BQ=y(km), 
(1)试写出y关于x的函数关系式,并求出x的取值范围;
(2)若B为公园入口,P,Q为观光车站,观光车站P位于线段AB靠近入口B的一侧.经测算,每天由B入口至观光车站P,Q乘坐观光车的游客数量相等,均为1万人,问如何确定观光车站P,Q的位置,使所有游客步行距离之和最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com