
 (
(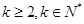 )的数列
)的数列 、
、 、
、 前
前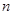 项的和分别为
项的和分别为 、
、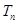 、
、 .已知集合
.已知集合 =
= .
. ,求数列
,求数列 的通项公式;
的通项公式;
 ,试研究
,试研究 和
和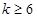 时是否存在符合条件的数列对(
时是否存在符合条件的数列对( ,
, ),并说明理由;
),并说明理由; ,对于固定的
,对于固定的 ,求证:符合条件的数列对(
,求证:符合条件的数列对( ,
, )有偶数对.
)有偶数对. ;(2)
;(2) 时,数列
时,数列 、
、 可以为(不唯一)6,12,16,14;2,8,10,4,
可以为(不唯一)6,12,16,14;2,8,10,4,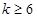 时,数列对(
时,数列对( ,
, )不存在.(3)证明见解析.
)不存在.(3)证明见解析.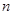 项和
项和 ,要求通项公式
,要求通项公式 的问题,利用关系
的问题,利用关系 来解决;(2)
来解决;(2) 时,可求出
时,可求出 ,再利用
,再利用
 ,可找到数列对(
,可找到数列对( ,
, )(注意结果不唯一),当
)(注意结果不唯一),当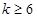 时,由于
时,由于 ,即
,即 ,可以想象,若存在,则
,可以想象,若存在,则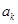 应该很大(体现在
应该很大(体现在 ),研究发现
),研究发现 (具体证明可利用二项展开式,
(具体证明可利用二项展开式,


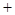

 ,注意到
,注意到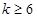 ,展开式中至少有7项,故
,展开式中至少有7项,故 ,下面证明这个式子大于
,下面证明这个式子大于 ,应该很好证明了),这不符合题意,故不存在;(3)可通过构造法说明满足题意和数列对是成对出现的,即对于数列对(
,应该很好证明了),这不符合题意,故不存在;(3)可通过构造法说明满足题意和数列对是成对出现的,即对于数列对( ,
, ),构造新数列对
),构造新数列对 ,
,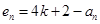 (
( ),则数列对(
),则数列对(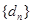 ,
, )也满足题意,(要说明的是
)也满足题意,(要说明的是 及
及 =
= 且数列
且数列 与
与 ,
, 与
与 不相同(用反证法,若相同,则
不相同(用反证法,若相同,则 ,又
,又 ,则有
,则有 均为奇数,矛盾).
均为奇数,矛盾). 时,
时,
 时,
时, ,
, 不适合该式
不适合该式 4分
4分 ,
, 时,
时,
 6分
6分 时,
时, ,
, ,
, ,
,
 =
=
 、
、 可以为(不唯一):
可以为(不唯一):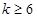 时,
时,


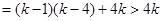
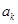 不存在.故数列对(
不存在.故数列对( ,
, )不存在. 10分
)不存在. 10分
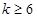 时,
时,

 ,
,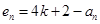 (
( ) 12分
) 12分
 =
= ,得
,得

 ,
, )与(
)与( ,
, )成对出现。 16分
)成对出现。 16分 与
与 相同,则由
相同,则由 及
及 ,得
,得 ,
, ,均为奇数,矛盾!
,均为奇数,矛盾! ,
, )有偶数对。 18分
)有偶数对。 18分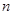 项和
项和 与
与 的关系;(2)观察法,二项展开式证明不等式;(3)构造法.
的关系;(2)观察法,二项展开式证明不等式;(3)构造法.

 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:不详 题型:解答题
 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有
 ,其中
,其中 为数列
为数列 的前
的前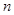 项和.
项和. 、
、 ;
; 的通项公式;
的通项公式; ,对任意的
,对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
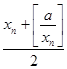 (n∈N*).现有下列命题:
(n∈N*).现有下列命题: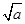 -1;
-1;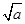 ].
].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com