
在极坐标系内,已知曲线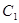 的方程为
的方程为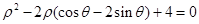 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为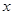 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线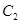 的参数方程为
的参数方程为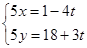 (
( 为参数).
为参数).
(1)求曲线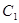 的直角坐标方程以及曲线
的直角坐标方程以及曲线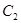 的普通方程;
的普通方程;
(2)设点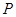 为曲线
为曲线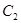 上的动点,过点
上的动点,过点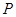 作曲线
作曲线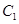 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
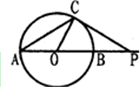 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试理科数学试卷(解析版) 题型:解答题
在极坐标系内,已知曲线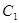 的方程为
的方程为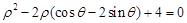 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
(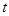 为参数).
为参数).
(1) 求曲线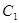 的直角坐标方程以及曲线
的直角坐标方程以及曲线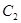 的普通方程;
的普通方程;
(2) 设点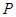 为曲线
为曲线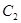 上的动点,过点
上的动点,过点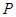 作曲线
作曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试文科数学试卷(解析版) 题型:解答题
在极坐标系内,已知曲线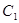 的方程为
的方程为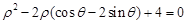 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为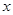 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线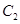 的参数方程为
的参数方程为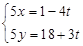 (
(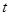 为参数).
为参数).
(1) 求曲线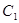 的直角坐标方程以及曲线
的直角坐标方程以及曲线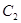 的普通方程;
的普通方程;
(2) 设点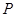 为曲线
为曲线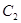 上的动点,过点
上的动点,过点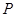 作曲线
作曲线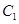 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com