
【题目】某电视台问政直播节目首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A部门 | 50% | 25% | 25% |
B部门 | 80% | 0 | 20% |
C部门 | 50% | 50% | 0 |
D部门 | 40% | 20% | 40% |

(1)若市民甲选择的是A部门,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的市民中再选出2人进行电视访谈,求这两人中至少有一人选择的是D部门的概率.
【答案】(1)0.1(2)![]()
【解析】
(1)由条形统计图中可以得到市民代表共200人,其中负责问政A部门的市民为40人,又由分层抽样20份求出从A部门问卷中抽取了4份,继而得到甲的调查问卷被选中的概率
(2)分别计算出分层抽样20份中负责问政A,B,C,D四部门的市民人数,其中可以得到不满意的人数,用枚举法列出符合条件的情况,然后求出结果
解:(1)由条形图可得,分别负责问政A,B,C,D四个管理部门的现场市民代表共有200人,其中负责问政A部门的市民为40人.
由分层抽样可得从A部门问卷中抽取了![]() 份.设事件M=“市民甲被选中进行问卷调查”,所以
份.设事件M=“市民甲被选中进行问卷调查”,所以![]() .
.
∴若甲选择的是A部门,甲被选中问卷调查的概率是0.1.
(2)由图表可知,分别负责问政A,B,C,D四部门的市民被选中进行问卷调查的人数为4,5,6,5.其中不满意的人数分别为1,1,0,2个.记对A部门不满意的市民是a;对B部门不满意的市民是b;对D部门不满意的市民是c,d.
设事件N=“从填写不满意的市民中选出2人,至少有一人选择的是D”.
从填写不满意的市民中选出2人,共有(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共6个基本事件;而事件N有(a,c),(a,d),(b,c),(b,d),(c,d)共5个基本事件,所以![]() .
.
∴这两人中至少有一人选择的是D的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】以下结论错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
C.命题“若![]() ,则
,则![]() 有实根”的逆命题为真命题
有实根”的逆命题为真命题
D.命题“![]() ,则
,则![]() 或
或![]() ”的否命题是“
”的否命题是“![]() ,则
,则![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为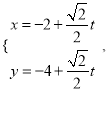 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com