
设函数f(x)满足2f(x)-f(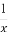 )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
(1)求f(x)的解析式.
(2)求{bn}的通项公式bn.
(3)试比较2an与bn的大小,并证明你的结论.
(1) f(x)=2x+1 (2) bn=3·2n-2 (3)见解析
【解析】(1)∵2f(x)-f( )=4x-
)=4x-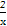 +1,
+1,
∴2f( )-f(x)=
)-f(x)=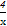 -2x+1.
-2x+1.
联立方程组
①×2+②,得3f(x)=6x+3
∴f(x)=2x+1.
(2)由题设an+1=2an+2n+1 ③,
an+2=2an+1+2n+3 ④,
④-③得an+2-an+1=2(an+1-an)+2,
即bn+1=2bn+2,∴bn+1+2=2(bn+2),
∴{bn+2}为等比数列.
q=2,b1=a2-a1=4,bn+2=6·2n-1,
∴bn=3·2n-2.
(3)由(2),知an+1-an=3×2n-2,而已知an+1-2an=2n+1,联立解得an=3×2n-2n-3,
∴2an=6×2n-4n-6,
∴2an-bn=3×2n-4(n+1).
当n=1时,2a1-b1=-2<0,∴2a1<b1;
当n=2时,2a2-b2=0,∴2a2=b2;
当n=3时,2a3-b3=8>0,∴2a3>b3;
当n=4时,2a4-b4=28>0,∴2a4>b4.
猜想当n≥3时,2an>bn即3×2n>4(n+1).
当n=3时,显然成立,
假设当n=k(k≥3)时,命题正确,
即3×2k>4(k+1).
当n=k+1时,
即3×2k+1=2×(3×2k)>8(k+1)=8k+8
=4k+8+4k>4k+8=4(k+2).
不等式也成立,故对一切n≥3且n∈N*,
2an>bn.
综上所述,当n=1时,2an<bn;
当n=2时,2an=bn;
当n≥3时,2an>bn.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
若α,β是两个相交平面,点A不在α内,也不在β内,则过点A且与α和β都平行的直线( )
(A)只有1条 (B)只有2条
(C)只有4条 (D)有无数条
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:填空题
将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D -ABC的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
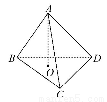
已知ABCD为四面体,O为△BCD内一点(如图),则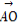 =
= (
(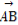 +
+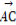 +
+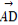 )是O为△BCD的重心的( )
)是O为△BCD的重心的( )
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
如图,在底面为平行四边形的四棱柱ABCD - A1B1C1D1中,M是AC与BD的交点,若 =a,
=a,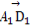 =b,
=b,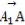 =c,则下列向量中与
=c,则下列向量中与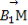 相等的向量是( )
相等的向量是( )
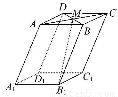
(A)- a+
a+ b+c (B)
b+c (B) a+
a+ b+c (C)
b+c (C) a-
a- b+c (D)-
b+c (D)- a-
a- b+c
b+c
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:填空题
用数学归纳法证明:(n+1)+ (n+2)+…+(n+n)=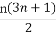 (n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
某个命题与正整数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得
(A)n=6时该命题不成立 (B)n=6时该命题成立
(C)n=4时该命题不成立 (D)n=4时该命题成立
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
已知函数f(x)=( )x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:
)x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为 .(将你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:解答题
已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求cos3(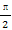 -θ)+sin3(
-θ)+sin3(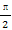 -θ)的值.
-θ)的值.
(2)求tan(π-θ)-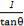 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com