
分析 运用三棱锥的棱长的关系,求解线段,面积,体积,把三棱锥镶嵌在长方体中,求解外接圆的半径,
解答 解:对于①,∵△ABC的三边长分别为AB=5,BC=4,AC=3,
∴PM丄平面ABC,且M是AB边中点,∴MA=MB=MC
∴Rt△PMA≌Rt△PMB≌Rt△PMC,∴PA=PB=PC,∴①正确,
对于②,∵当PC⊥面ABC,∴△PCM面积=$\frac{1}{2}$×PC×CM=$\frac{1}{2}$×5×CM
又因为CM作为垂线段最短=$\frac{12}{5}$,△PCM面积的最小值为$\frac{1}{2}×5×\frac{12}{5}$=6,∴②不正确.
对于③,∵若PB=5,PB⊥平面ABC,AB=5,BC=4,AC=3,
∴三棱锥P-ABC的外接球可以看做3,4,5为棱长的长方体,∴2R=5$\sqrt{2}$,∴体积为$\frac{125\sqrt{2}}{3}π$,故③不正确.
对于④,∵△ABC的外接圆的圆心为O,PO⊥面ABC,∵P2=PO2+OC2,r=$\frac{3+4-5}{2}$=1,
OC=$\sqrt{2}$,PO2=25-2=23,PO=$\sqrt{23}$,
$\frac{1}{3}×\frac{1}{2}$××3×4×$\sqrt{23}$=2$\sqrt{23}$,故④正确
故答案为:①④
点评 本题考查了空间直线,几何体的性质,位置关系,求解面积,夹角问题,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+2y-1=0 | B. | 3x+2y+7=0 | C. | 2x-3y+5=0 | D. | 2x-3y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2] | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
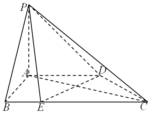 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数的图象一定过原点 | B. | y=x2+1(-4<x≤4)是偶函数 | ||
| C. | y=|x+1|-|x-1|是奇函数 | D. | y=x+1是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com