
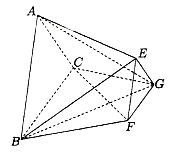
【题目】如图,三棱台![]() 的底面是正三角形,平面
的底面是正三角形,平面![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,易证四边形
,易证四边形![]() 为平行四边形,即
为平行四边形,即![]() ,由于
,由于![]() ,
,![]() 为
为![]() 的中点,可得到
的中点,可得到![]() ,从而得到
,从而得到![]() ,即可证明
,即可证明![]() 平面
平面![]() ,从而得到
,从而得到![]() ;(Ⅱ)易证
;(Ⅱ)易证![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,求出平面
,求出平面![]() 的一个法向量为
的一个法向量为![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() ,即可得到答案。
,即可得到答案。
解:(Ⅰ)取![]() 的中点为
的中点为![]() ,连结
,连结![]() .
.
由![]() 是三棱台得,平面
是三棱台得,平面![]() 平面
平面![]() ,从而
,从而![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)连结![]() .
.
由![]() 是正三角形,且
是正三角形,且![]() 为中点,则
为中点,则![]() .
.
由(Ⅰ)知,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
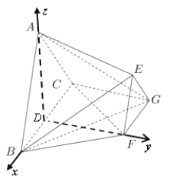
以![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由 可得,
可得,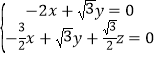 .
.
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 务极点,
务极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
,![]()
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求以
,求以![]() 为直径的圆与
为直径的圆与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学毕业生参加一个公司的招聘考试,考试分笔试和面试两个环节,笔试有![]() 、
、![]() 两个题目,该学生答对
两个题目,该学生答对![]() 、
、![]() 两题的概率分别为
两题的概率分别为![]() 、
、![]() ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为![]() ,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
(1)求该学生被公司聘用的概率;
(2)设该学生应聘结束后答对的题目或问题的总个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B、任务C不能相邻,则不同的执行方案共有( )
A. 36种B. 44种C. 48种D. 54种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若![]() ,则
,则![]()
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,点
,点![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com