
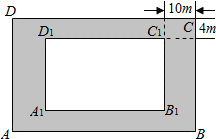
 ��ͼ��ij���ز�������˾�ƻ���һ¥���ڽ���һ�������ι�ABCD�����ɳ����ε�������A1B1C1D1�ͻ������е�����Ӱ���֣���ɣ���֪���е��Ŀ��ֱ�Ϊ4m��10m
��ͼ��ij���ز�������˾�ƻ���һ¥���ڽ���һ�������ι�ABCD�����ɳ����ε�������A1B1C1D1�ͻ������е�����Ӱ���֣���ɣ���֪���е��Ŀ��ֱ�Ϊ4m��10m ���� ��1������������A1B1C1D1�����Ϊ4000ƽ���ף���ʾ��C1B1=$\frac{4000}{x}$�ף������ɵù�ABCD��ռ���S����x�ĺ���S��x���Ľ���ʽ�����û�������ʽȷ������ռ��С��������ɵõ����ۣ�
��2����AB=x����BC=$\frac{4000}{x}$�ף�A1B1=x-20�ף�C1B1=$\frac{4000}{x}$-8�ף��ɵ�������A1B1C1D1�����S����x�ĺ���S��x���Ľ���ʽ�����û�������ʽȷ������ռ��С��������ɵõ����ۣ�
��� �⣺��1����A1B1=x�ף�֪C1B1=$\frac{4000}{x}$��
��S=��x+20����$\frac{4000}{x}$+8��=4160+8x+$\frac{80000}{x}$��4160+2$\sqrt{8x•\frac{80000}{x}}$=5760
���ҽ���8x=$\frac{80000}{x}$����x=100ʱȡ�Ⱥ�
��Ҫʹ����ռ�����С��������A1B1C1D1�ij�Ϊ100�ס���Ϊ40�ף�
��2����AB=x����BC=$\frac{4000}{x}$�ף���A1B1=x-20�ף�C1B1=$\frac{4000}{x}$-8��
��S=��x-20����$\frac{4000}{x}$-8��=4160-8x-$\frac{80000}{x}$��4160+2$\sqrt{8x•\frac{80000}{x}}$=5760
���ҽ���8x=$\frac{80000}{x}$����x=100ʱȡ�Ⱥ�
��Ҫʹ������A1B1C1D1���������ij�Ϊ100�ס���Ϊ40�ף�
���� ���⿼�麯��ģ�͵Ĺ����������������ʽ�����ã�ע��ʹ��������һ����������ȣ�


 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
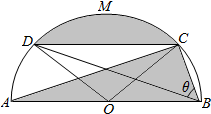 ��ͼ����Ӱ������һ����е�������ù�������һ���Բ����Ƥ���к�ʣ���˹�����CMD����������ABC���γɵģ����а�Բֱ��AB=8��CD��AB����M��$\widehat{CD}$��һ�㣬��CBD=�ȣ�
��ͼ����Ӱ������һ����е�������ù�������һ���Բ����Ƥ���к�ʣ���˹�����CMD����������ABC���γɵģ����а�Բֱ��AB=8��CD��AB����M��$\widehat{CD}$��һ�㣬��CBD=�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com