
【题目】下面四个命题:
①![]() 在定义域上单调递增;
在定义域上单调递增;
②若锐角![]() ,
,![]() 满足
满足![]() ,则
,则![]() ;
;
③![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() ;
;
④函数![]() 的一个对称中心是
的一个对称中心是![]() ;
;
其中真命题的序号为______.
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y/千亿元 | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的线性回归方程![]() t+
t+![]() ;
;
(2)用所求回归方程预测该地区2018年(t=6)的人民币储蓄存款.
附:回归方程![]() t+
t+![]() 中,
中, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)某电视台举办的闯关节目共有五关,只有通过五关才能获得奖金,规定前三关若有失败即结束,后两关若有失败再给一次从失败的关开始继续向前闯的机会(后两关总共只有一次机会),已知某人前三关每关通过的概率都是![]() ,后两关每关通过的概率都是
,后两关每关通过的概率都是![]() .
.
(1)求该人获得奖金的概率;
(2)设该人通过的关数为X,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C:![]() .
.
![]() 若圆C的切线l在x轴和y轴上的截距相等,且截距不为零,求切线l的方程;
若圆C的切线l在x轴和y轴上的截距相等,且截距不为零,求切线l的方程;
![]() 已知点
已知点![]() 为直线
为直线![]() 上一点,由点P向圆C引一条切线,切点为M,若
上一点,由点P向圆C引一条切线,切点为M,若![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,2mx2+mx-![]() <0,命题q:2m+1>1.若“p∧q”为假,“p∨q”为真,则实数m的取值范围是( )
<0,命题q:2m+1>1.若“p∧q”为假,“p∨q”为真,则实数m的取值范围是( )
A. (-3,-1)∪[0,+∞) B. (-3,-1]∪[0,+∞)
C. (-3,-1)∪(0,+∞) D. (-3,-1]∪(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次高中学科知识竞赛中,对4000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
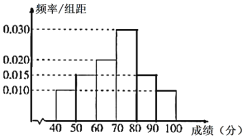
A.成绩在![]() 的考生人数最多B.不及格的考生人数为1000
的考生人数最多B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约为70D.考生竞赛成绩的中位数为75分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点A,B的坐标分别为(-2,0),(2,0)直线AM,BM相交于点M,且它们的斜率之积是-![]() .
.
(1)求点M的轨迹E的方程;
(2)设直线l:y=kx与E交于C,D两点,F1(-1,0),F2(1,0),若E上存在点P,使得![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是以
是以![]() 为直径的圆上两点,
为直径的圆上两点,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,将圆沿直径
,将圆沿直径![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 的射影
的射影![]() 在
在![]() 上,已知
上,已知![]() .
.

(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求证:![]()
![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
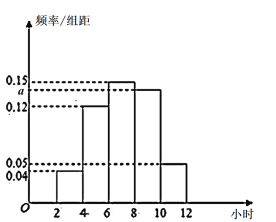
(1)估计这100名学生参加实践活动时间的众数、中位数和平均数.
(2)估计这100名学生参加实践活动时间的上四分位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com