
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)圆心![]() 的轨迹
的轨迹![]() :
: ![]() ;
;
(2)![]() 和
和![]() 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为![]() ;
;
(3)当![]() 时,
时, ![]() 取最大值
取最大值![]() .
.
【解析】试题分析:(1)根据两圆相切得圆心距与半径之间关系: 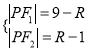 ,消去半径得
,消去半径得![]() ,符合椭圆定义,由定义可得轨迹方程(2)探究问题,实质是计算问题,即利用坐标求
,符合椭圆定义,由定义可得轨迹方程(2)探究问题,实质是计算问题,即利用坐标求![]() 和
和![]() 的比值:根据直线方程与椭圆方程联立方程组,利用两点间距离公式及韦达定理、弦长公式可得
的比值:根据直线方程与椭圆方程联立方程组,利用两点间距离公式及韦达定理、弦长公式可得![]() 和
和![]() 的表达式,两式相比即得比值
的表达式,两式相比即得比值![]() (3)因为
(3)因为![]() 的面积
的面积![]() 的面积,所以
的面积,所以![]() ,利用原点到直线距离得三角形的高,而底为弦长MN(2中已求),可得面积表达式,为一个分式函数,结合变量分离法(整体代换)、基本不等式求最值
,利用原点到直线距离得三角形的高,而底为弦长MN(2中已求),可得面积表达式,为一个分式函数,结合变量分离法(整体代换)、基本不等式求最值
试题解析:解:(1)设圆心![]() 的坐标为
的坐标为![]() ,半径为
,半径为![]() ,
,
由于动圆![]() 一圆
一圆![]() 相切,且与圆
相切,且与圆![]() 相内切,所以动圆
相内切,所以动圆![]() 与圆
与圆![]() 只能内切
只能内切
∴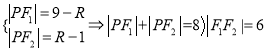
∴圆心![]() 的轨迹为以
的轨迹为以![]() 为焦点的椭圆,其中
为焦点的椭圆,其中![]() ,
,
∴![]()
故圆心![]() 的轨迹
的轨迹![]() .
.
(2)设![]() ,直线
,直线![]() ,则直线
,则直线![]() ,
,
由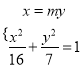 可得:
可得: 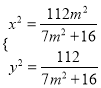 ,∴
,∴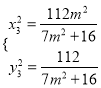 ,
,
∴![]()
由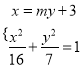 可得:
可得: ![]() ,
,
∴![]() ,
,
∴![]()
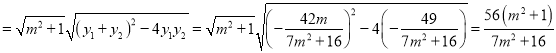 .
.
∴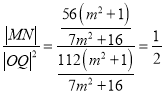
∴![]() 和
和![]() 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为![]() .
.
(3)∵![]() ,∴
,∴![]() 的面积
的面积![]() 的面积,∴
的面积,∴![]() ,
,
∵![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴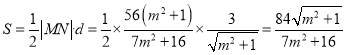 .1
.1
令![]() ,则
,则![]() ,
, 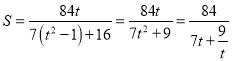 ,
,
∵![]() (当且仅当
(当且仅当![]() ,即
,即![]() ,亦即
,亦即![]() 时取等号)
时取等号)
∴当![]() 时,
时, ![]() 取最大值
取最大值![]() .1
.1


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB. (Ⅰ)求角B的大小;
acosB. (Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是梯形.四边形
是梯形.四边形![]() 是矩形.且平面
是矩形.且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的动点.
上的动点.
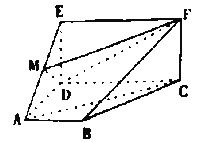
(Ⅰ)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积= ![]() (弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为
(弦×矢+矢2).弧田,由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长,“矢”等于半径长与圆心到弦的距离之差,按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为 ![]() π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为 .
π,弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)﹣b(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是 ![]() ,若将f(x)的图象先向右平移
,若将f(x)的图象先向右平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位,所得函数g(x)为奇函数.
个单位,所得函数g(x)为奇函数.
(1)求f(x)的解析式;
(2)求f(x)的对称轴及单调区间;
(3)若对任意x∈[0, ![]() ],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12. 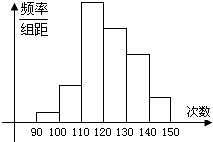
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com