
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是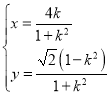 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的取值范围.
的距离的取值范围.
科目:高中数学 来源: 题型:
【题目】古代数学名著《九章算术》中记载:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除,即三个面是等腰梯形,两侧面是直角三角形的五面体我们教室打扫卫生用的灰斗近似于一个羡除,又有所不同.如图所示,ABCD是一个矩形,ABEF和CDFE都是等腰梯形,且平面ABCD⊥平面ABEF,AB=30,BC=10,EF=50,BE=26.则这个灰斗的体积是( )
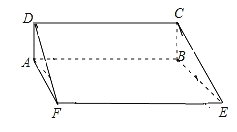
A.3600B.4000C.4400D.4800
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,下图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
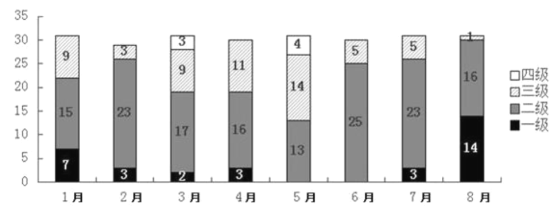
①1月至8月空气合格天数超过24天的月份有3个
②第二季度与第一季度相比,空气合格天数的比重下降了
③8月是空气质量最好的一个月
④6月的空气质量最差
A.②③B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
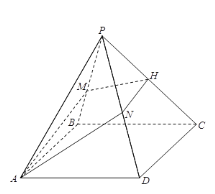
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
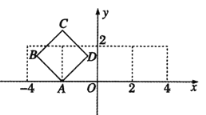
【题目】在平面直角坐标系![]() 中,如图放置的边长为2的正方形ABCD沿
中,如图放置的边长为2的正方形ABCD沿![]() 轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点
轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
A.函数![]() 在
在![]() 上有两个零点
上有两个零点
B.函数![]() 是偶函数
是偶函数
C.函数![]() 在
在![]() 上单调递增
上单调递增
D.对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 的投影为
的投影为![]() 的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥
的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥![]() 的内切球的表面积为( )
的内切球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com