
【题目】在直角坐标系xoy中,曲线C1的参数方程为 ![]() ,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=4
)=4 ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值. 其中正确的是________.
,无最大值. 其中正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等比数列,公比为q(q>0且q≠1),4a1 , 3a2 , 2a3成等差数列,且它的前4项和为S4=15.
(1)求{an}通项公式;
(2)令bn=an+2n(n=1,2,3…),求{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆E: ![]() +
+ ![]() =1(a>b>0)的焦点到直线x﹣3y=0的距离为
=1(a>b>0)的焦点到直线x﹣3y=0的距离为 ![]() ,离心率为
,离心率为 ![]() ,抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点与E交于A,B,与G交于C,D.
,抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点与E交于A,B,与G交于C,D.
(1)求椭圆E及抛物线G的方程;
(2)是否存在学常数λ,使 ![]() 为常数,若存在,求λ的值,若不存在,说明理由.
为常数,若存在,求λ的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
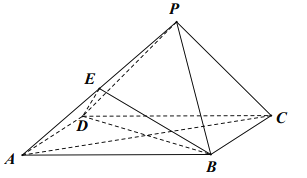
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
(1)求椭圆方程;
(2)过点![]() 且不垂直于坐标轴的直线与椭圆交于
且不垂直于坐标轴的直线与椭圆交于![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com