分析:(Ⅰ)由图象可知:导函数在x=-3和x=1处函数值为0,原函数在x=1处取到极小值-5,转化为方程组即可解到a、b、c的值,可知函数解析式;
(Ⅱ)f(x)≥x
3-3lnx+m对任意的
x∈[,e]都恒成立,?m≤3x
2-9x+3lnx对任意的
x∈[,e]都恒成立,故只需m小于等于3x
2-9x+3lnx在
x∈[,e]的最小值,然后用导数法求函数在闭区间的最值即可.
解答:解:(Ⅰ)∵f(x)=ax
3+bx
2+cx∴f'(x)=3ax
2+2bx+c,
由图象可知:导函数在x=-3和x=1处函数值为0,原函数在x=1处取到极小值-5,
故
| | f′(-3)=27a-6b+c=0 | | f′(1)=3a+2b+c=0 | | f(1)=a+b+c=-5 |
| |
解此方程组得a=1,b=3,c=-9.
∴f(x)=x
3+3x
2-9x.…(5分)
(Ⅱ)由题意f(x)≥x
3-3lnx+m对任意的
x∈[,e]都恒成立,?m≤3x
2-9x+3lnx对任意的
x∈[,e]都恒成立,
故只需m小于等于3x
2-9x+3lnx在
x∈[,e]的最小值.
令?(x)=3x
2-9x+3lnx,
x∈[,e],则
?′(x)=6x-9+==
,
令?'(x)=0,解得
x1=,x
2=1,当x变化时,?(x),?'(x)的变化情况如下表:
| x |
|
(,) |
|
(,1) |
1 |
(1,e) |
e |
| ?'(x) |
|
+ |
0 |
- |
0 |
+ |
|
| ?(x) |
φ() |
|
极大值 |
|
极小值-6 |
|
?(e) |
∵
?()=--3>-6=?(1),∴?(x)在x=1处取得
x∈[,e]的最小值?(1)=-6,∴m≤-6.
故m的取值范围为:m≤-6 …(12分)
点评:本题为导数的综合应用,涉及解三元一次方程组和导数法求闭区间的最值,属难题.

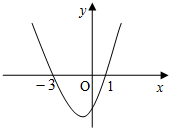 设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.
设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.
