
 时,不等式
时,不等式 成立;
成立; 成立,能否将条件“
成立,能否将条件“ ”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由;
”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由; 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立, 且
且 .
. 且
且 ,
, ,
, ,
, .
.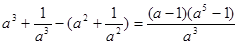 ,
, ,
, 
 ,
, 成立.
成立. 且
且 ,式子
,式子 与
与 同号,恒成立,
同号,恒成立, 且
且 .
. 且
且 ,
, ,
, ,
, .
.
 .
. ,则由
,则由 不等式成立;
不等式成立; ,则由
,则由 不等式成立.
不等式成立. 且
且 ,
, ,
, ,
, 成立.
成立. 且
且 ,
, ,
, 也对.
也对.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com