
| x2 |
| 3 |
| y2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| x12 |
| 3 |
| y12 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| x2 |
| 3 |
| y2 |
| 2 |
| 6km |
| 3k2+2 |
| 3(m2- 2) |
| 3k2+2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
2
| ||||
| 3k2+2 |
| |m| | ||
|
| 1 |
| 2 |
| 1+k2 |
2
| ||||
| 3k2+2 |
| |m| | ||
|
| ||||
| 3k2+2 |
| ||
| 2 |
| 6km |
| 3k2+2 |
| 3(m2- 2) |
| 3k2+2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 6 |
| x1+x2 |
| 2 |
| 3k |
| 2m |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| -3k2+2m2 |
| 2m |
| 1 |
| m |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 9k2 |
| 4m2 |
| 1 |
| m2 |
| 6m2-2 |
| 4m2 |
| 1 |
| 2 |
| 1 |
| m2 |
| 24(3k2+2-m2) |
| ( 2+3k2)2 |
| 2(2m2-1) |
| m2 |
| 1 |
| m2 |
| 1 |
| 2 |
| 1 |
| m2 |
| 1 |
| m2 |
| 1 |
| m2 |
| 1 |
| m2 |
3-
| ||||
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| 1 |
| m2 |
| 1 |
| m2 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |


 АйЗжбЇЩњзївЕБОЬтСЗЭѕЯЕСаД№АИ
АйЗжбЇЩњзївЕБОЬтСЗЭѕЯЕСаД№АИ ЛЅЖЏПЮЬУЯЕСаД№АИ
ЛЅЖЏПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 8 |
| 3 |
| Іа |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 8 |
| 3 |
| Іа |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2012ФъМЊСжЪЁИпПМЪ§бЇЗТецФЃФтЪдОэ3ЃЈРэПЦЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
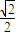 ЕФЭждВCЃК
ЕФЭждВCЃК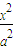 +
+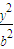 =1ЃЈaЃОbЃО0ЃЉЙ§ЕуMЃЈ
=1ЃЈaЃОbЃО0ЃЉЙ§ЕуMЃЈ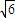 ЃЌ1ЃЉЃЌOЮЊзјБъдЕуЃЎ
ЃЌ1ЃЉЃЌOЮЊзјБъдЕуЃЎ ЕФвЛЬѕЧаЯпЃЌЪджЄУїЁЯAOB=
ЕФвЛЬѕЧаЯпЃЌЪджЄУїЁЯAOB=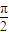 ЃЎЫќЕФФцУќЬтГЩСЂТ№ЃПШєГЩСЂЃЌЧыИјГіжЄУїЃЛЗёдђЃЌЧыЫЕУїРэгЩЃЎ
ЃЎЫќЕФФцУќЬтГЩСЂТ№ЃПШєГЩСЂЃЌЧыИјГіжЄУїЃЛЗёдђЃЌЧыЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2011ФъЩНЖЋЪЁИпПМЪ§бЇЪдОэЃЈРэПЦЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
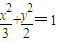 НЛгкPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉСНВЛЭЌЕуЃЌЧвЁїOPQЕФУцЛ§SЁїOPQ=
НЛгкPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉСНВЛЭЌЕуЃЌЧвЁїOPQЕФУцЛ§SЁїOPQ=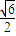 ЃЌЦфжаOЮЊзјБъдЕуЃЎ
ЃЌЦфжаOЮЊзјБъдЕуЃЎ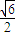 ЃПШєДцдкЃЌХаЖЯЁїDEGЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌХаЖЯЁїDEGЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com