


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:044
已知曲线C的方程是(t+1) +2at)x+3at+b=0,直线l的
+2at)x+3at+b=0,直线l的
方程是y=t(x-1),若对任意实数t,曲线C恒过定点P(1,0).
(1)求定值a,b;
(2)直线l截曲线C所得弦长为d,记f(t)= ,则当t为何值时,f(t)有最大值,最大值是多少?
,则当t为何值时,f(t)有最大值,最大值是多少?
(3)若点M( )在曲线C上,又在直线l上,求
)在曲线C上,又在直线l上,求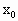 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:广西柳铁一中2012届高三第四次月考数学理科试题 题型:044
设函数f(x)=x2+ax+b(a,b∈R),若函数在点(1,f(1))处的切线为4x―y―16=0,数列{an}、{bn}定义:![]() .
.
(1)求实数a、b的值;
(2)若将数列{bn}的前n项的和与积分别记为Sn、Tn.证明:对任意正整数n,![]() 为定值;证明:对任意正整数n,都有
为定值;证明:对任意正整数n,都有 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:①方程y=kx+2可表示经过点(0,2)的所有直线;②经过点P(x0,y0)且与直线l:![]() 垂直的直线方程一定能写成B(x-x0)-A(y-y0)=0的形式;③对任意实数α,直线
垂直的直线方程一定能写成B(x-x0)-A(y-y0)=0的形式;③对任意实数α,直线![]() 总与某一定圆相切;④过定圆M上的定占A作圆的动弦AB,若
总与某一定圆相切;④过定圆M上的定占A作圆的动弦AB,若![]() ,则动点P的轨迹为椭圆,其中所有真命题的序号为 .
,则动点P的轨迹为椭圆,其中所有真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:①方程y=kx+2可表示经过点(0,2)的所有直线;②经过点P(x0,y0)且与直线l:![]() 垂直的直线方程一定能写成B(x-x0)-A(y-y0)=0的形式;③对任意实数α,直线
垂直的直线方程一定能写成B(x-x0)-A(y-y0)=0的形式;③对任意实数α,直线![]() 总与某一定圆相切;④过定圆M上的定点A作圆的动弦AB,若
总与某一定圆相切;④过定圆M上的定点A作圆的动弦AB,若![]() ,则动点P的轨迹为椭圆,其中所有真命题的序号为 .
,则动点P的轨迹为椭圆,其中所有真命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com