
【题目】已知向量 ![]() =(2sinx,
=(2sinx, ![]() cosx),
cosx), ![]() =(﹣sinx,2sinx),函数f(x)=
=(﹣sinx,2sinx),函数f(x)= ![]()
![]() .
.
(1)求f(x)的单调递增区间;
(2)求函数f(x)在区间[0, ![]() ]的最值及所对应的x值.
]的最值及所对应的x值.
【答案】
(1)解:向量 ![]() =(2sinx,
=(2sinx, ![]() cosx),
cosx), ![]() =(﹣sinx,2sinx),
=(﹣sinx,2sinx),
函数f(x)= ![]()
![]()
=﹣2sin2x+2 ![]() sinxcosx
sinxcosx
=﹣2× ![]() +
+ ![]() sin2x
sin2x
= ![]() sin2x+cos2x﹣1
sin2x+cos2x﹣1
=2sin(2x+ ![]() )﹣1;
)﹣1;
根据正弦函数的图象与性质,
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
所以函数f(x)的单调递增区间是[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
(2)解:当x∈[0, ![]() ]时,2x+
]时,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
所以sin(2x+ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
所以sin(2x+ ![]() )﹣1∈[﹣
)﹣1∈[﹣ ![]() ,0],
,0],
所以当x= ![]() 时,函数f(x)在区间[0,
时,函数f(x)在区间[0, ![]() ]上取得最小值﹣
]上取得最小值﹣ ![]() ,
,
x= ![]() 时,函数f(x)取得最大值0
时,函数f(x)取得最大值0
【解析】根据平面向量的数量积求出f(x)的解析式,(1)根据正弦函数的图象与性质,求出函数f(x)的单调递增区间;(2)求出x∈[0, ![]() ]时sin(2x+
]时sin(2x+ ![]() )的取值,从而求出函数f(x)在区间[0,
)的取值,从而求出函数f(x)在区间[0, ![]() ]上的最值以及对应x的值.
]上的最值以及对应x的值.
【考点精析】关于本题考查的正弦函数的单调性,需要了解正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能得出正确答案.
上是减函数才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+px+q.求证:
(1)f(1)+f(3)-2f(2)=2;
(2)|f(1)|,|f(2)|,|f(3)|中至少有一个不小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:
(1)AD应取多长?
(2)容器的容积为多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2008奥运会上两名射击运动员甲、乙在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax﹣ ![]() ﹣5lnx,其中a∈R.
﹣5lnx,其中a∈R.
(1)若g(x)在其定义域内为增函数,求正实数a的取值范围;
(2)设函数h(x)=x2﹣mx+4,当a=2时,若x1∈(0,1),x2∈[1,2],总有g(x1)≥h(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
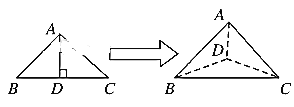
①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣ ![]() (a>0)
(a>0)
(1)若x=1是函数f(x)的一个极值点,求a的值;
(2)若f(x)≥0在[0,+∞)上恒成立,求a的取值范围;
(3)证明: ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2﹣2x+2﹣a2)(a>0),g(x)=x2+6x+c(c∈R).
(1)若曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣4x﹣2,求a的值;
(2)求函数f(x)的单调区间;
(3)当a=1时,对x1∈[﹣2,2],x2∈[﹣2,2],使f(x1)<g(x2)成立,求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com