练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设lg2x-lgx2-2=0的两根是α、β，则logαβ+logβα的值是（ ）
    A．-4
    B．-2
    C．1
    D．3
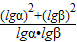
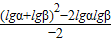
    【答案】分析：由lg2x-lgx2-2=0的两根是α、β，知lgα+lgβ=1，lgα•lgβ=-2，所以logαβ+logβα===，由此能求出其结果．
    解答：解：∵lg2x-lgx2-2=0的两根是α、β，
    ∴lgα+lgβ=2，lgα•lgβ=-2，
    logαβ+logβα=
    =
    =
    =
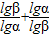
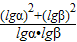
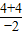
    =-4．
    故选A．
    点评：本题考查对数的运算性质，解题时要认真审题，注意韦达定理的灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设lg2x-lgx2-2=0的两根为α，β，则logαβ+logβα=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设lg2x-lgx2-2=0的两根是α、β，则logαβ+logβα的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设lg2x-lgx2-2=0的两根是α、β，则logαβ+logβα的值是（　　）
    A．-4B．-2C．1D．3

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省镇江九中高三（上）期中数学试卷（理科）（解析版） 题型：填空题

    设lg2x-lgx2-2=0的两根为α，β，则logαβ+logβα=    ．

    查看答案和解析>>

    同步练习册答案