
【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为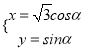 .
.
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为![]() ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
【答案】(1)点P在直线l上;(2)![]() .
.
【解析】试题分析:(1)消去曲线![]() 参数方程中的参数,得到曲线
参数方程中的参数,得到曲线![]() 普通方程,根据公式
普通方程,根据公式![]() ,把点
,把点![]() 的坐标化为直角坐标方程,即可判断点
的坐标化为直角坐标方程,即可判断点![]() 与直线
与直线![]() 的关系;(2)设
的关系;(2)设![]() ,由点到直线的距离公式可得距离的表达式,通过三角恒等变换化为正弦型函数在给定区间上的最值来求解.
,由点到直线的距离公式可得距离的表达式,通过三角恒等变换化为正弦型函数在给定区间上的最值来求解.
试题解析:(1)∵曲线C的参数方程为 ,
,
∴曲线C的普通方程是![]() ,
,
∵点P的极坐标为![]() ,
,
∴点P的普通坐标为(4cos![]() ,4sin
,4sin![]() ),即(0,4),
),即(0,4),
把(0,4)代入直线l:x﹣y+4=0,
得0﹣4+4=0,成立,
故点P在直线l上.
(2)∵Q在曲线C: 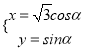 上,(0°≤α<360°)
上,(0°≤α<360°)
∴![]() 到直线l:x﹣y+4=0的距离:
到直线l:x﹣y+4=0的距离:
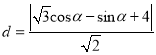
=![]() ,(0°≤α<360°)
,(0°≤α<360°)
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
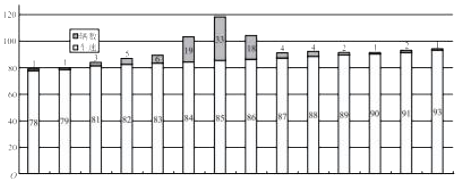
经计算:样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于![]() 或车速大于
或车速大于![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2)从样本中任取![]() 个车辆,求这
个车辆,求这![]() 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;
(3)从该快速车道上所有车辆中任取![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
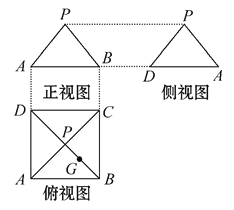
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.
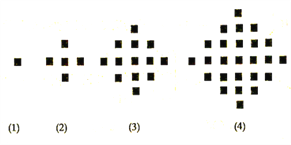
(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品上市30天内每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是
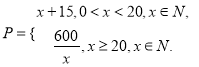 该商品的日销售量
该商品的日销售量![]() 件与时间
件与时间![]() 天函数关系是
天函数关系是
![]() .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;
(2)求这个商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少![]() ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的![]() ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com