
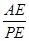 的值;
的值;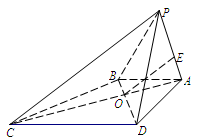
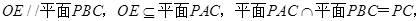 所以
所以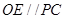 ,再结合平面几何的知识易得:
,再结合平面几何的知识易得: 结合比例线段关系即可求得
结合比例线段关系即可求得 ;(2)中要证明面面垂直,根据面面垂直的判定定理可转化为证明线面垂直,由题中的数量关系不难发现取
;(2)中要证明面面垂直,根据面面垂直的判定定理可转化为证明线面垂直,由题中的数量关系不难发现取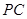 的中点
的中点 ,连结
,连结 ,运用解三角形的知识算出
,运用解三角形的知识算出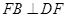 ,问题即可得证.
,问题即可得证. 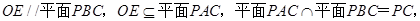 所以
所以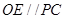 ,
, . 3分
. 3分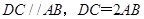 ,所以
,所以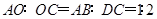 .
. . 6分
. 6分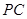 的中点
的中点 ,连结
,连结 .
.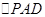 是正三角形,
是正三角形,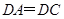 ,所以
,所以 .
. 为
为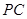 的中点,所以
的中点,所以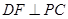 . 8分
. 8分 ,所以
,所以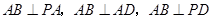 .
. ,所以
,所以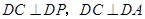 .
.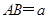 ,在等腰直角三角形
,在等腰直角三角形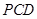 中,
中, .
.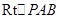 中,
中,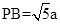 .
. 中,
中,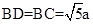 .
.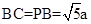 ,点F为PC的中点,所以
,点F为PC的中点,所以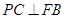 .
.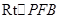 中,
中,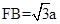 .
. 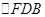 中,由
中,由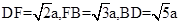 ,可知
,可知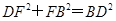 ,所以
,所以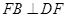 .
.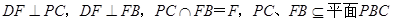 ,所以
,所以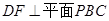 .
.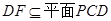 ,所以平面
,所以平面 14分
14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题

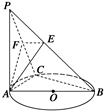
| A.平面ABC⊥平面ABD |
| B.平面ABD⊥平面BDC |
| C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE |
| D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 |
| B.1 |
| C.2 |
| D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
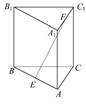
A.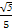 | B.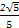 | C. | D.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com