
【题目】已知函数f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围.
【答案】
(1)解:a= ![]() 时,f(x)=
时,f(x)= ![]() xln(x+1)+x+1,
xln(x+1)+x+1,
f′(x)= ![]() [ln(x+1)+1﹣
[ln(x+1)+1﹣ ![]() ]+1,
]+1,
∵f′(x)在(﹣1,+∞)递增,且f′(﹣1+ ![]() )=0,
)=0,
故x∈(﹣1,﹣1+ ![]() )时,f′(x)<0,f(x)递减,
)时,f′(x)<0,f(x)递减,
x∈(﹣1+ ![]() ,+∞)时,f′(x)>0,f(x)递减,
,+∞)时,f′(x)>0,f(x)递减,
故f(x)在(﹣1,﹣1+ ![]() )递减,在(﹣1+
)递减,在(﹣1+ ![]() ,+∞);
,+∞);
(2)解:记g(x)=f(x)﹣ex(x≥0),g(0)=0,
则g′(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,
]+1﹣ex,
记h(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,
]+1﹣ex,
h′(x)=a[ 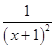 +
+ ![]() ]﹣ex,h′(0)=2a﹣1,
]﹣ex,h′(0)=2a﹣1,
①a≤ ![]() 时,∵
时,∵ 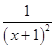 +
+ ![]() ∈(0,2],ex≥1,
∈(0,2],ex≥1,
∴h′(x)≤0,h(x)在(0,+∞)递减,
则h(x)≤h(0)=0,即g′(x)≤0,∴g(x)在(0,+∞)递减,
∴g(x)≤g(0)=0恒成立,即f(x)≤ex恒成立,满足题意;
②a≥ ![]() 时,h′(x)在(0,+∞)递减,
时,h′(x)在(0,+∞)递减,
又h′(0)=2a﹣1>0,x→+∞时,h′(x)→﹣∞,
则必存在x0∈(0,+∞),使得h′(x0)=0,
则x∈(0,x0)时,h′(x)>0,h(x)在(0,x0)递增,
此时h(x)>h(0)=0,
x∈(0,x0)时,g′(x)>0,∴g(x)在(0,x0)递增,
∴g(x)>g(0)=0,即f(x)>ex,不合题意,
综上,a≤ ![]() .
.
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)记g(x)=f(x)﹣ex(x≥0),g(0)=0,求出函数的导数,记h(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,通过讨论a的范围,求出函数的单调性,从而确定a的具体范围即可.
]+1﹣ex,通过讨论a的范围,求出函数的单调性,从而确定a的具体范围即可.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】设集合A={x1 , x2 , x3 , x4},xi∈{﹣1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
A.60
B.65
C.80
D.81
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1的一个焦点为F(2,0),且离心率为
=1的一个焦点为F(2,0),且离心率为 ![]()
(1)求椭圆方程;
(2)过点M(3,0)作直线与椭圆交于A,B两点,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.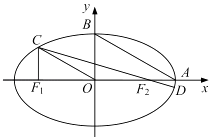
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且 ![]() ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 ![]() 的最小值为 .
的最小值为 . 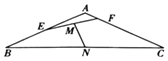
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别为角ABC所对的边,且 ![]() acosC=csinA.
acosC=csinA.
(1)求角C的大小.
(2)若c=2 ![]() ,且△ABC的面积为6
,且△ABC的面积为6 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com