
【题目】已知函数![]() ,
, ![]() 满足关系
满足关系![]() (其中
(其中![]() 是常数).
是常数).
(![]() )如果
)如果![]() ,
, ![]() ,求函数
,求函数![]() 的值域;
的值域;
(![]() )如果
)如果![]() ,
, ![]() ,且对任意
,且对任意![]() ,存在
,存在![]() ,
, ![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(![]() )如果
)如果![]() ,求函数
,求函数![]() 的最小正周期(只需写出结论).
的最小正周期(只需写出结论).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆![]() 的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如下图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
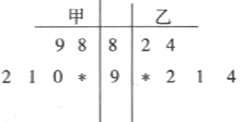
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com