
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 在底面
在底面![]() 上的射影为底面
上的射影为底面![]() 的中心点
的中心点![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() 的面积为1.
的面积为1.
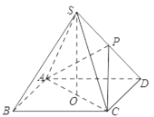
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在点![]() 符合题意,点
符合题意,点![]() 为棱
为棱![]() 靠近端点
靠近端点![]() 的三等分点
的三等分点
【解析】
(1)利用等腰三角形“三线合一”证明![]() 平面
平面![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() ;
;
(2)分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,利用平面的法向量求二面角,进而计算得到
,利用平面的法向量求二面角,进而计算得到![]() 即可
即可
(1)∵点![]() 在底面
在底面![]() 上的射影为点
上的射影为点![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵四边形![]() 是边长为
是边长为![]() 的正方形,∴
的正方形,∴![]() ,
,
∵三角形![]() 的面积为1,∴
的面积为1,∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴![]() ,同理可得
,同理可得![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
(2)存在,
如图,连接![]() ,易得
,易得![]() 两两互相垂直,
两两互相垂直,
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
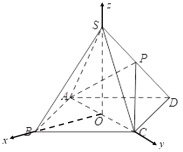
则![]() ,假设存在点
,假设存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ,
,
不妨设![]() ,
,
∵点![]() 在棱
在棱![]() 上,∴
上,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则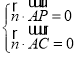 ,∴
,∴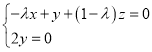 ,
,
令![]() ,可得
,可得![]() ,∴平面
,∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,
,
∴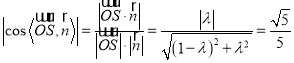 ,即
,即![]() ,
,
解得![]() 或
或![]() (舍)
(舍)
所以存在点![]() 符合题意,点
符合题意,点![]() 为棱
为棱![]() 靠近端点
靠近端点![]() 的三等分点
的三等分点


科目:高中数学 来源: 题型:
【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.![]() 年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了
年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了![]() 个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为
个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为![]() 表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
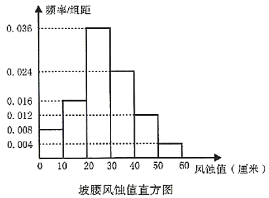
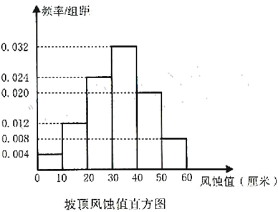
(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于![]() ”的概率;
”的概率;
(Ⅱ)若一个插钎的风蚀值小于![]() ,则该数据要标记“
,则该数据要标记“![]() ”,否则不标记根据以上直方图,完成列联表:
”,否则不标记根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“
的把握认为数据标记“![]() ”与沙丘上插钎所布设的位置有关?
”与沙丘上插钎所布设的位置有关?
附: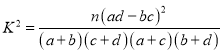 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂根据市场需求开发三角花篮支架(如图),上面为花篮,支架由三根细钢管组成,考虑到钢管的受力和花篮质量等因素,设计支架应满足:①三根细钢管长均为1米(粗细忽略不计),且与地面所成的角均为![]() ;②架面与架底平行,且架面三角形
;②架面与架底平行,且架面三角形![]() 与架底三角形
与架底三角形![]() 均为等边三角形;③三根细钢管相交处的节点
均为等边三角形;③三根细钢管相交处的节点![]() 分三根细钢管上、下两段之比均为
分三根细钢管上、下两段之比均为![]() .定义:架面与架底的距离为“支架高度”,架底三角形
.定义:架面与架底的距离为“支架高度”,架底三角形![]() 的面积与“支架高度”的乘积为“支架需要空间”.
的面积与“支架高度”的乘积为“支架需要空间”.
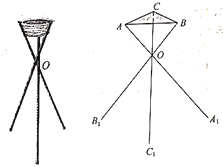
(1)当![]() 时,求“支架高度”;
时,求“支架高度”;
(2)求“支架需要空间”的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
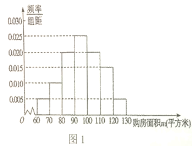
【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:万元/平方米,
(单位:万元/平方米,![]() 进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价
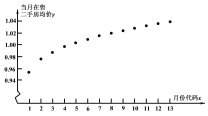
进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价![]() (单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房面积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如下表所示:
,并得到一些统计量的值,如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.00050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: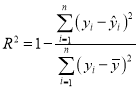 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到其中所有正确结论的编号是( )
个单位得到其中所有正确结论的编号是( )
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1F2,右顶点为A,P为椭圆C上任意一点.已知
的左右焦点分别为F1F2,右顶点为A,P为椭圆C上任意一点.已知![]() 的最大值为3,最小值为2.
的最大值为3,最小值为2.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C相交于MN两点(MN不是左右顶点),且以MN为直径的圆过点A.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,点A为曲线
,点A为曲线![]() 上的动点,点B在线段OA的延长线上,且满足
上的动点,点B在线段OA的延长线上,且满足![]() ,点B的轨迹为
,点B的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点C的极坐标为(2,0),求△ABC面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com