
分析 (1)由$\frac{x-1}{x+1}$≠0,x+1≠0,解得即可得出函数f(x)的定义域;计算f(-x)与±f(x)的关系,即可判断出.
(2)函数f(x)在区间(-1,1)上的减函数.利用单调性的证明方法即可证明.
解答 解:(1)由$\frac{x-1}{x+1}$≠0,x+1≠0,解得x≠±1.
∴函数f(x)的定义域为{x|x∈R,x≠±1}.
f(-x)=$lo{g}_{a}|\frac{-x-1}{-x+1}|$=-$lo{g}_{a}|\frac{x-1}{x+1}|$=-f(x),
∴函数f(x)在定义域上是奇函数.
(2)函数f(x)在区间(-1,1)上的减函数.
证明:?x1,x2∈(-1,1),且x1<x2.
则f(x1)-f(x2)=$lo{g}_{a}\frac{1-{x}_{1}}{1+{x}_{2}}$-$lo{g}_{a}\frac{1-{x}_{2}}{1+{x}_{2}}$=$lo{g}_{a}\frac{(1-{x}_{1})(1+{x}_{2})}{(1+{x}_{1})(1-{x}_{2})}$,
∵(1-x1)(1+x2)-(1+x1)(1-x2)=2(x2-x1)>0,
(1-x1)(1+x2)>0,(1+x1)(1-x2)>0.
∴$\frac{(1-{x}_{1})(1+{x}_{2})}{(1+{x}_{1})(1-{x}_{2})}$>1.
∴$lo{g}_{a}\frac{(1-{x}_{1})(1+{x}_{2})}{(1+{x}_{1})(1-{x}_{2})}$>0,
∴f(x1)>f(x2).
∴函数f(x)在区间(-1,1)上的减函数.
点评 本题考查了单调性的证明方法、奇偶性的判定方法、对数的运算性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>0,bc>0 | B. | ab>0,bc<0 | C. | ab<0,bc>0 | D. | ab<0,bc<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
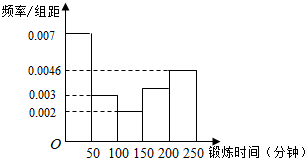 某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.
某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.| “勤于锻炼者” | 非“勤于锻炼者” | 合计 | |
| 男 | 25 | 70 | |
| 女 | |||
| 合计 |
| p(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com