[题目]设不等式-2<|x-1|-|x+2|<0的解集为M .a,b∈M .(Ⅰ)证明:||<, (Ⅱ)比较|1-4ab|与2|a-b|的大小.并说明理由. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设不等式-2<|x-1|-|x+2|<0的解集为M ，a,b∈M .

（Ⅰ）证明：||<；

（Ⅱ）比较|1-4ab|与2|a-b|的大小，并说明理由.

【答案】(Ⅰ)证明见解析；(Ⅱ)答案见解析.

【解析】试题分析：

(1)首先求得集合M，然后结合绝对值不等式的性质即可证得题中的结论；

(2)利用平方做差的方法可证得|1-4ab|＞2|a-b|.

试题解析：

（Ⅰ）证明：记f (x) =|x-1|-|x+2|，

则f(x)= ，所以解得-＜x＜，故M=(-,).

所以，||≤|a|+|b|＜×+×=.

（Ⅱ）由（Ⅰ）得0≤a2＜，0≤b2＜.

|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)=4(a2-1)(b2-1)>0.

所以，|1-4ab|＞2|a-b|.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）对任意的x，y∈R，总有f（x）+f（y）=f（x+y），且x＜0时，f（x）＞0．
（1）求证：函f（x）是奇函数；
（2）求证：函数f（x）是R上的减函数；
（3）若定义在（﹣2，2）上的函数f（x）满足f（﹣m）+f（1﹣m）＜0，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}满足al=﹣2，an+1=2an+4．

（I）证明数列{an+4}是等比数列；

（Ⅱ）求数列{|an|}的前n项和Sn．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax3+ +4，（a≠0，b≠0），则f（2）+f（﹣2）= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校举行“庆元旦”教工羽毛球单循环比赛（任意两个参赛队伍只比赛一场），有高一、高二、高三共三个队参赛，高一胜高二的概率为，高一胜高三的概率为，高二胜高三的概率为，每场胜负相互独立，胜者记1分，负者记0分，规定：积分相同时，高年级获胜.

（1）若高三获得冠军的概率为，求；

（2）记高三的得分为，求的分布列和期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】海南省椰树集团引进德国净水设备的使用年限（年）和所需要的维修费用y（千元）的几组统计数据如表：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

（1）请根据上表提供的数据，用最小二乘法求出关于x的线性回归方程；
（2）我们把中（1）的线性回归方程记作模型一，观察散点图发现该组数据也可以用函数模型 =c1ln（c2x）拟合，记作模型二．经计算模型二的相关指数R2=0.64，
①请说明R2=0.64这一数据在线性回归模型中的实际意义．
②计算模型一中的R2的值（精确到0.01），通过数据说明，两种模型中哪种模型的拟合效果好．
参考公式和数值：用最小工乘法求线性回归方程系数公式 = 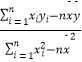，．R2=1﹣ 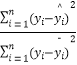， =0.651，（2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3）