
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.

【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
试题
(Ⅰ)要证线面平行,就要证线线平行,考虑到![]() 是
是![]() 中点,因此取
中点,因此取![]() 中点
中点![]() ,可得
,可得![]() 与
与![]() 平行且相等,从而可证得
平行且相等,从而可证得![]() ,所以可证得线面平行;
,所以可证得线面平行;
(Ⅱ)求二面角,可建立空间直角坐标系,用向量法求解,考虑到平面![]() 与平面
与平面![]() 垂直,
垂直,![]() 是菱形,因此取
是菱形,因此取![]() 中点
中点![]() ,则有
,则有![]() ,因此
,因此![]() ,所以可作
,所以可作![]() ,以
,以![]() 为
为![]() 轴建立空间直角坐标系,写出各点坐标,求出二面角两个面的法向量,由法向量的夹角可得二面角;
轴建立空间直角坐标系,写出各点坐标,求出二面角两个面的法向量,由法向量的夹角可得二面角;
(Ⅲ)在(Ⅱ)的坐标系,利用已知![]() 得
得![]() 点坐标,从而可得向量
点坐标,从而可得向量![]() 的坐标,利用向量
的坐标,利用向量![]() 与平面
与平面![]() 的法向量夹角的正弦值可求得
的法向量夹角的正弦值可求得![]() ,最后可得
,最后可得![]() 的长度.
的长度.
试题解析:
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ∥
∥![]() ∥
∥![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形
为平行四边形
所以![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
则![]() ∥平面
∥平面![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() 因为平面
因为平面![]()
![]() 平面
平面![]() ,交线为
,交线为![]() ,则
,则![]() 平面
平面![]()
作![]() ∥
∥![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,如图,
轴建立空间直角坐标系,如图,

则![]()
于是![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则![]() 令
令![]() ,则
,则![]()
平面![]() 的法向量
的法向量![]()
所以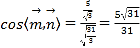
又因为二面角![]() 为锐角,所以其余弦值为
为锐角,所以其余弦值为![]() .
.
(Ⅲ)![]() 则
则![]() ,
,
![]() ,而平面
,而平面![]() 的法向量为
的法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
于是![]()
于是![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com