[题目]分形几何学是美籍法国数学家伯努瓦曼德尔布罗特( )在20世纪70年代创立的一门新学科.它的创立为解决传统众多领域的难题提供了全新的思路.下图是按照分型的规律生长成的一个树形图.则第10行的空心圆的个数是．题目和参考答案——青夏教育精英家教网—

【题目】分形几何学是美籍法国数学家伯努瓦曼德尔布罗特（）在20世纪70年代创立的一门新学科，它的创立为解决传统众多领域的难题提供了全新的思路.下图是按照分型的规律生长成的一个树形图，则第10行的空心圆的个数是__________．

【答案】21.

【解析】分析：根据图形分析相邻两行黑圆、空心圆的个数关系，得到两者间的关系，逐步计算得出第10行的空心圆的个数.

详解：根据图中的分形规律可知，1个空心圆分形为1个黑圆，1个黑圆分形为1个空心圆1个黑圆，白球个数记为点的横坐标，黑圆个数记为纵坐标，所以第一行记为（1，0），第二行记为（0，1），第三行记为（1，1），第四行记为（1，2）；第五行记为（2，3）∴由此可以归纳出下一行的空心圆个数就是上一行的黑圆的个数，下一行的黑圆的个数就是上一行的黑圆、空心圆的个数和，所以由此可得第10行的空心圆的个数是21.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）若，求函数的值域；

（2）讨论函数的奇偶性，并说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2+a（x+lnx），a∈R．（Ⅰ）若当a=﹣1时，求f（x）的单调区间；
（Ⅱ）若f（x）＞（e+1）a，求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，且

（1）求的解析式；

（2）若存在，使得成立，求的取值范围；

（3）证明函数的图象在图象的下方.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】掷2个骰子，至少有一个1点的概率为（用数字作答）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图4，四边形ABCD为菱形，∠ABC=60°．PA⊥平面ABCD，E为PC中点．
（Ⅰ）求证：平面BED⊥平面ABCD；
（Ⅱ）求平面PBA与平面EBD所成二面角（锐角）的余弦值．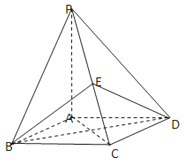

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】中国古代儒家要求学生掌握六种基本才艺：礼、乐、射、御、书、数，简称“六艺”，某中学为弘扬“六艺”的传统文化，分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛，现有甲、乙、丙三位选手进入了前三名的最后角逐、规定：每场知识竞赛前三名的得分都分别为（，且）；选手最后得分为各场得分之和，在六场比赛后，已知甲最后得分为26分，乙和丙最后得分都为11分，且乙在其中一场比赛中获得第一名，则下列推理正确的是（）