【答案】
分析:(1)在△F
1PF
2中,MO为中位线,根据三角形的中位线定理再结合椭圆的定义即可得出答案.
(2)先利用椭圆的定义得|PF
1|+|PF
2|=10,在△PF
1F
2中利用余弦定理得cos 60°=
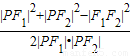
,两者结合即可求得|PF
1|•|PF
2|.
(3)由点P(x,y)处的焦半径公式|PF
1|=5+

x,|PF
2|=5-

x,知|PF
1|•|PF
2|=25-
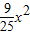
,再由|x|≤5,能求出|PF
1|•|PF
2|的最值.
解答:(1)证明:在△F
1PF
2中,
∵MO为中位线,
∴|MO|=
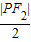
=
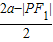
=a-
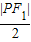
=5-

|PF
1|….(3分)
(2)解:∵|PF
1|+|PF
2|=10,
∴|PF
1|
2+|PF
2|
2=100-2|PF
1|•|PF
2|,
在△PF
1F
2中,cos 60°=
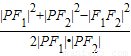
,
∴|PF
1|•|PF
2|=100-2|PF
1|•|PF
2|-36,
∴|PF
1|•|PF
2|=
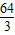
.…(8分)
(3)解:由点P(x,y)处的焦半径公式|PF
1|=5+

x,|PF
2|=5-

x,
∴|PF
1|•|PF
2|=25-
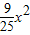
,
∵|x|≤5,∴0≤x
2≤25,
∴16≤|PF
1|•|PF
2|≤25.
∴|PF
1|•|PF
2|的最小值为16,|PF
1|•|PF
2|的最大值为25.
点评:本题考查直线与圆锥曲线的综合运用,具体涉及到椭圆的简单性质、余弦定理、焦半径等基本知识点,解题时要认真审题,注意等价转化思想的合理运用.

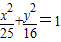 上一点,左、右焦点分别为F1,F2.
上一点,左、右焦点分别为F1,F2.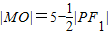 ;
;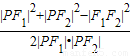 ,两者结合即可求得|PF1|•|PF2|.
,两者结合即可求得|PF1|•|PF2|. x,|PF2|=5-
x,|PF2|=5- x,知|PF1|•|PF2|=25-
x,知|PF1|•|PF2|=25-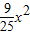 ,再由|x|≤5,能求出|PF1|•|PF2|的最值.
,再由|x|≤5,能求出|PF1|•|PF2|的最值.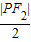 =
=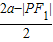 =a-
=a-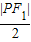 =5-
=5- |PF1|….(3分)
|PF1|….(3分)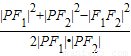 ,
,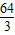 .…(8分)
.…(8分) x,|PF2|=5-
x,|PF2|=5- x,
x,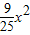 ,
,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案