
���� ��ԲC��$\frac{x^2}{25}+\frac{y^2}{9}=1$�Ľ���ΪF1��-4��0����F2��4��0��������˵㣺����5��0��������˵㣺��0����3����
����$\sqrt{25-k-��9-k��}$=4���ɵô���Բ����ԲC�Ľ�����ͬ�������жϳ�����
��˫���ߵĽ�������ԲC �ij���Ķ˵㣬��������ԲC�Ľ��㣬���ɵó�������̣������жϳ�����
����$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$����PO���ӳ�������Բ�ཻ�ڵ�Q�����ı���PF1QF2�Ǿ��Σ����$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}}|$=|F1F2|=8�������жϳ�����
����A��x1��y1����B��x2��y2����ֱ��AB���̣�my=x-4������Բ����������Ϊ��9m2+25��y2+72my-81=0�����ø���ϵ���Ĺ�ϵ����$\overrightarrow{AF}=3\overrightarrow{FB}$��-y1=3y2��������m�����ɵó�k��
��� �⣺��ԲC��$\frac{x^2}{25}+\frac{y^2}{9}=1$�Ľ���ΪF1��-4��0����F2��4��0��������˵㣺����5��0��������˵㣺��0����3����
������$\frac{x^2}{25-k}+\frac{y^2}{9-k}={1_{\;}}��k��9��$����$\sqrt{25-k-��9-k��}$=4���ɵô���Բ����ԲC�Ľ�����ͬ����ȷ��
��˫���ߵĽ�������ԲC �ij���Ķ˵㣬��������ԲC�Ľ��㣬���������Ϊ$\frac{x^2}{16}-\frac{y^2}{9}=1$����ȷ��
������PΪ��Բ��һ�㣬������$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$����PO���ӳ�������Բ�ཻ�ڵ�Q�����ı���PF1QF2�Ǿ��Σ����$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}}|$=|F1F2|=8����ȷ��
����A��x1��y1����B��x2��y2����ֱ��AB���̣�my=x-4������$\left\{\begin{array}{l}{my=x-4}\\{\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1}\end{array}\right.$����Ϊ��9m2+25��y2+72my-81=0����y1+y2=-$\frac{72m}{9{m}^{2}+25}$��y1y2=$\frac{-81}{9{m}^{2}+25}$����*��
��$\overrightarrow{AF}=3\overrightarrow{FB}$����-y1=3y2�����루*���ɵã�39m2=25��m��0�����m=$\frac{5}{\sqrt{39}}$����k=$\frac{\sqrt{39}}{5}$����˲���ȷ��
�������о�������ȷ������Ǣ٢ڢۣ�
�ʴ�Ϊ���٢ڢۣ�
���� ���⿼����Բ���ߵı����̼������ʡ����������ж���������������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $log_4^{0.3}��{0.4^3}��{3^{0.4}}$ | B�� | ${0.4^3}��log_4^{0.3}��{3^{0.4}}$ | ||
| C�� | $log_4^{0.3}��{3^{0.4}}��{0.4^3}$ | D�� | ${0.4^3}��{3^{0.4}}��log_4^{0.3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
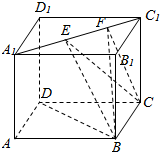 ��ͼ���ⳤΪ1��������ABCD-A1B1C1D1�У�E��FΪA1C1�ϵĶ��㣬��EF=$\frac{1}{2}$�������н����д�����ǣ�������
��ͼ���ⳤΪ1��������ABCD-A1B1C1D1�У�E��FΪA1C1�ϵĶ��㣬��EF=$\frac{1}{2}$�������н����д�����ǣ�������| A�� | BD��CE | |
| B�� | ��CEF�����Ϊ��ֵ | |
| C�� | ������BCEF�������EF��λ�õı仯���仯 | |
| D�� | ֱ��BE��CFΪ����ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��a��b | B�� | c��b��a | C�� | a��b��c | D�� | a��c��b |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com