
【题目】某公司的两个部门招聘工作人员,应聘者从 T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题 T1 , 且表示只要成绩合格就签约;丙、丁两人选择使用试题 T2 , 并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是 ![]() ,丙、丁考试合格的概率都是
,丙、丁考试合格的概率都是 ![]() ,且考试是否合格互不影响.
,且考试是否合格互不影响.
(1)求丙、丁未签约的概率;
(2)记签约人数为 X,求 X的分布列和数学期望EX.
【答案】
(1)解:分别记事件甲、乙、丙、丁考试合格为 A,B,C,D.
由题意知 A,B,C,D相互独立,且 ![]() ,
, ![]() .
.
记事件“丙、丁未签约”为F,
由事件的独立性和互斥性得:
P(F)=1﹣P(CD)
= ![]()
(2)解:X的所有可能取值为0,1,2,3,4.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以,X的分布列是:
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
X的数学期望 ![]()
【解析】(1)分别记事件甲、乙、丙、丁考试合格为 A,B,C,D.由题意知 A,B,C,D相互独立,且 ![]() ,
, ![]() .记事件“丙、丁未签约”为F,由事件的独立性和互斥性得能求出丙、丁未签约的概率.(2) X的所有可能取值为0,1,2,3,4,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
.记事件“丙、丁未签约”为F,由事件的独立性和互斥性得能求出丙、丁未签约的概率.(2) X的所有可能取值为0,1,2,3,4,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0, ![]() <φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为
<φ<π)部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为 ![]() ,则f(﹣1)=( )
,则f(﹣1)=( ) 
A.﹣2
B.2
C.- ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
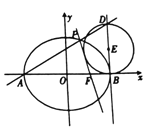
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品最近30天的价格f(t)(元)与时间t满足关系式:f(t)= 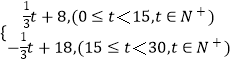 ,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是![]() .
.
(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量![]() 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求![]() 分布列及期望.
分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请A片区房源的概率;
(2)申请的房源所在片区的个数的ξ分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,(a∈R)
(1)若函数f(x)在点区间[e,+∞]处上为增函数,求a的取值范围;
(2)若函数f(x)的图象在点x=e(e为自然对数的底数)处的切线斜率为3,且k∈Z时,不等式 k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值;
(3)n>m≥4时,证明:(mnn)m>(nmm)n .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com