
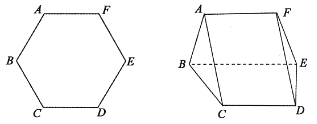
【题目】如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且![]() ,(1)证明:平面ABEF
,(1)证明:平面ABEF![]() 平面BCDE; (2)求DE与平面ABC所成角的正弦值。
平面BCDE; (2)求DE与平面ABC所成角的正弦值。
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)连接AC、BE,交点为G,推导出![]() 从而AG⊥平面BCDE,由此能证明平面ABEF⊥平面BCDE.
从而AG⊥平面BCDE,由此能证明平面ABEF⊥平面BCDE.
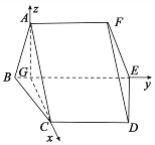
(2)以G为坐标原点,分别以GC,GE,GA所在的直线为x轴,y轴,z轴建立如图所示的坐标系,利用向量法能求出FE与平面ABC所成角的正弦值.
试题解析:
(1)证明:正六边形ABCDEF中,连接AC、BE,交点为G,易知![]() ,且
,且![]() ,
,
在多面体中,由![]() ,知
,知![]() ,故
,故![]()
又![]()
![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,
又![]() 平面ABEF,所以平面ABEF
平面ABEF,所以平面ABEF![]() 平面BCDE.
平面BCDE.
(2)以G为坐标原点,分别以GC,GE,GA所在的直线为x轴,y轴,z轴建立如图所示的坐标系.
由![]() ,
, ![]() ,
, ![]() ,
,
则![]()
![]() .
.
![]() ,
, ![]() ,
,
![]() ,
,
设平面ABC的法向量为![]() ,
,
则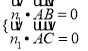 ,即
,即 ,令
,令 ![]() ,得
,得![]() ,
,
所以, ![]()
所以FE与平面ABC所成角的正弦值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,下列数值排序正确的是( ) 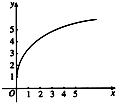
A.0<f′(2)<f′(3)<f(3)﹣f(2)
B.0<f′(3)<f(3)﹣f(2)<f′(2)
C.0<f(3)<f′(2)<f(3)﹣f(2)
D.0<f(3)﹣f(2)<f′(2)<f′(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=8y.AB是抛物线C的动弦,且AB过F(0,2),分别以A,B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C中心在原点,焦点在坐标轴上,且该椭圆经过点( ![]() ,
, ![]() )和点
)和点 ![]() .求
.求
(1)椭圆C的方程;
(2)P,Q,M,N四点在椭圆C上,F1为负半轴上的焦点,直线PQ,MN都过F1且 ![]() ,求四边形PMQN的面积最小值和最大值.
,求四边形PMQN的面积最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x2+x+1>0,命题q:x∈Q,x2=3,则下列命题中是真命题的是( )
A.p∧q
B.¬p∨q
C.¬p∧¬q
D.¬p∨¬q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,焦点在x轴,且抛物线上点P(2,m)到焦点的距离为3,斜率为2的直线L与抛物线相交于A,B两点且|AB|=3 ![]() ,求抛物线和直线L的方程.
,求抛物线和直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com