
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°, 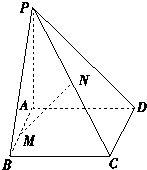
(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
【答案】
(1)证明:如图,取PD的中点E,连接AE,NE.

E、N分别为PD,PC的中点,
所以:EN∥CD, ![]() ,
,
又M为AB的中点,
所以: ![]() ,AM∥CD,
,AM∥CD,
EN∥AM,EN=AM,
所以:四边形AMNE为平行四边形.
MN∥AE,
所以:MN∥平面PAD,
PA⊥平面ABCD,∠PDA=45°,
所以:△PAD是等腰直角三角形,
所以:AE⊥PD.
又CD⊥AD,CD⊥PA,AD交PA于A,
所以:CD⊥平面PAD,AE平面PAD,
所以:CD⊥AE,
又CD交PD于D,
所以:AE⊥平面PCD,
则:MN⊥平面PCD
(2)若 PC⊥BD,又PA⊥BD,PA交PC于P,
所以:BD⊥平面PAC,
所以:BD⊥AC,即矩形ABCD的对角线互相垂直.
此时矩形为正方形.
即当矩形ABCD为正方形时,满足PC⊥BD.
【解析】(1)利用三角形的中位线得到线线平行,进一步得到线面平行,利用线线垂直进一步转化成线面垂直.(2)利用线面垂直转化线线垂直,最后确定矩形是正方形.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个. 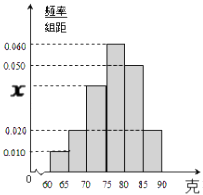
(Ⅰ)求样本容量;
(Ⅱ)若从净重在[60,70)克的产品中任意抽取2个,求抽出的2个产品恰好是净重在[65,70)的产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3+3x2﹣mx+1在[﹣2,2]上为单调增函数,则实数m的取值范围为( )
A.m≤﹣3
B.m≤0
C.m≥﹣24
D.m≥﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销该商品,可采用不同形式的分期付款,付款的期数![]() (单位:
(单位: ![]() )与商场经销一件商品的利润
)与商场经销一件商品的利润![]() (单位:元)满足如下关系:
(单位:元)满足如下关系: 
(Ⅰ)若记事件“购买该商品的3位顾客中,至少有1位采用一次性全额付款方式”为![]() ,试求事件
,试求事件![]() 的概率
的概率![]() ;
;
(Ⅱ)求商场经销一件商品的利润![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球.乙箱子里装有1个白球、2个黑球.每次游戏从这两个箱子里随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏结束后,①摸出3个白球的概率?②获奖的概率?
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为检验寒假学生自主学习的效果,年级部对某班50名学生各科的检测成绩进行了统计,下面是政治成绩的频率分布直方图,其中成绩分组区间是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求图中的![]() 值及平均成绩;
值及平均成绩;
(2)从分数在![]() 中选5人记为
中选5人记为![]() ,从分数在
,从分数在![]() 中选3人,记为
中选3人,记为![]() ,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求
,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1﹣x).
(1)在如图所给直角坐标系中画出函数f(x)的草图,并直接写出函数f(x)的零点;
(2)求出函数f(x)的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com