
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)若![]() 为等差数列,且
为等差数列,且![]()
①求该等差数列的公差![]() ;
;
②设数列![]() 满足
满足![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 最大?请说明理由;
最大?请说明理由;
(2)若![]() 还同时满足:
还同时满足:
①![]() 为等比数列;
为等比数列;
②![]() ;
;
③对任意的正整数![]() 存在自然数
存在自然数![]() ,使得
,使得![]() 、
、![]() 、
、![]() 依次成等差数列,试求数列
依次成等差数列,试求数列![]() 的通项公式.
的通项公式.
【答案】(1)①![]() ;②当
;②当![]() 或
或![]() 时,
时,![]() 最大;(2)
最大;(2)![]() .
.
【解析】
(1)①利用等差数列的通项公式及前![]() 项和公式,建立方程组,即可求得该等差数列的公差
项和公式,建立方程组,即可求得该等差数列的公差![]() ;
;
②求出![]() 的通项公式,进而得到
的通项公式,进而得到![]() 的通项公式,利用
的通项公式,利用![]() ,判断
,判断![]() 的单调性,进而得解;
的单调性,进而得解;
(2)根据等比数列的性质,并结合![]() ,初步确定
,初步确定![]() 的通项,再根据等差数列的性质,即可求得
的通项,再根据等差数列的性质,即可求得![]() 的通项公式.
的通项公式.
(1)①由![]() ,
,![]() ,
,
得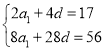 ﹐解得
﹐解得![]() ,
,![]() ,
,
该等差数列的公差![]() .
.
②由①知![]() ,所以
,所以![]() ,
,
则![]() ,
,
![]()
![]()
![]()
所以![]() ,且当
,且当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,
故当![]() 或
或![]() 时,
时,![]() 最大.
最大.
(2)因为![]() 是等比数列,则
是等比数列,则![]() ,
,
又![]() ,
,
所以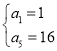 或
或 ,
,
由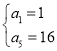 ,得
,得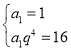 ,解得
,解得![]() ,
,
由 ,得
,得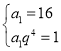 ,解得
,解得![]() ,
,
从而![]() 或
或![]() 或
或![]() 或
或![]() ,
,
又因为![]() 、
、![]() 、
、![]() 依次成等差数列,得
依次成等差数列,得![]() ,而公比
,而公比![]() ,
,
所以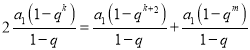 ,即
,即![]() ,
,
从而![]() (*)
(*)
当![]() 时,(*)式不成立;
时,(*)式不成立;
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,(*)式不成立;
时,(*)式不成立;
当![]() 时,(*)式不成立.
时,(*)式不成立.
综上所述,满足条件的![]() .
.


科目:高中数学 来源: 题型:
【题目】小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时,顾客从装有1个黑球,3个红球和6个白球(除颜色外其他都相同)的不透明的袋子中依次不放回地摸出3个球,根据摸出的球的颜色情况进行兑奖.顾客中一等奖,二等奖,三等奖,四等奖时分别可领取的奖金为![]() 元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:
元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:![]() 个黑球2个红球;
个黑球2个红球;![]() 个红球;
个红球;![]() 恰有1个白球;
恰有1个白球;![]() 恰有2个白球;
恰有2个白球;![]() 个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
(1)通过计算写出中一至四等奖分别对应的情况(写出字母即可);
(2)已知顾客摸出的第一个球是红球,求他获得二等奖的概率;
(3)设顾客抽一次奖小张获利![]() 元,求变量
元,求变量![]() 的分布列;若小张不打算在活动中亏本,求
的分布列;若小张不打算在活动中亏本,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 内部有一圆柱
内部有一圆柱![]() ,此圆柱恰好以直线
,此圆柱恰好以直线![]() 为轴.有下列命题:
为轴.有下列命题:
①圆柱![]() 的母线与正方体
的母线与正方体![]() 所有的棱所成的角都相等;
所有的棱所成的角都相等;
②正方体![]() 所有的面与圆柱
所有的面与圆柱![]() 的底面所成的角都相等;
的底面所成的角都相等;
③在正方体![]() 内作与圆柱
内作与圆柱![]() 底面平行的截面,则截面的面积
底面平行的截面,则截面的面积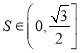 ;
;
④圆柱![]() 侧面积的最大值为
侧面积的最大值为![]() .
.
其中正确的命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 均相切,切点分别为
均相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于x的不等式
时,关于x的不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的是( )
的图象,则下列结论正确的是( )
①![]() 在R上单调递减
在R上单调递减
②![]() 的图像关于原点对称
的图像关于原点对称
③![]() 的图象上的点到坐标原点的距离的最小值为3
的图象上的点到坐标原点的距离的最小值为3
④函数![]() 不存在零点
不存在零点
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知某市穿城公路![]() 自西向东到达市中心
自西向东到达市中心![]() 后转向东北方向,
后转向东北方向,![]() ,现准备修建一条直线型高架公路
,现准备修建一条直线型高架公路![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,且要求市中心
,且要求市中心![]() 到
到![]() 所在的直线距离为
所在的直线距离为![]() .
.
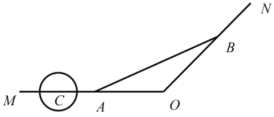
(1)求![]() ,
,![]() 两出入口间距离的最小值;
两出入口间距离的最小值;
(2)在公路![]() 段上距离市中心
段上距离市中心![]() 点
点![]() 处有一古建筑
处有一古建筑![]() (视为一点),现设立一个以
(视为一点),现设立一个以![]() 为圆心,
为圆心,![]() 为半径的圆形保护区,问如何在古建筑
为半径的圆形保护区,问如何在古建筑![]() 和市中心
和市中心![]() 之间设计出入口
之间设计出入口![]() ,才能使高架公路及其延长线不经过保护区?
,才能使高架公路及其延长线不经过保护区?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在
,点E在![]() 上,且
上,且![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如图2).
(如图2).
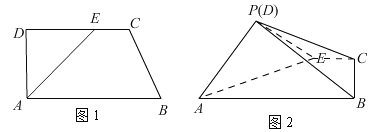
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点M,使
上是否存在点M,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,底面△
中,底面△![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
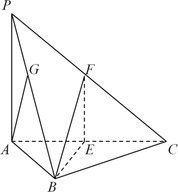
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得三棱锥
,使得三棱锥![]() 体积为
体积为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com