
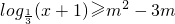 恒成立;命题q:对任意x∈
恒成立;命题q:对任意x∈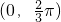 ,不等式
,不等式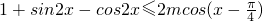 恒成立.
恒成立.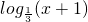 ,
,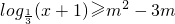 恒成立,等价于-2≥m2-3m,
恒成立,等价于-2≥m2-3m,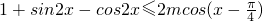 恒成立,
恒成立, m(sinx+cosx)恒成立,
m(sinx+cosx)恒成立,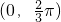 时,sinx+cosx为正,
时,sinx+cosx为正, sinx对任意x∈
sinx对任意x∈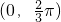 恒成立,
恒成立,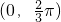 ,∴0<sinx≤1,0<
,∴0<sinx≤1,0< sinx≤
sinx≤


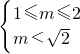 ,则1≤m<
,则1≤m< ;
;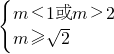 ,则m>2.
,则m>2. 或m>2,
或m>2, )∪(2,+∞).
)∪(2,+∞).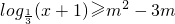 恒成立等价于m2-3m小于或等于
恒成立等价于m2-3m小于或等于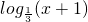 在x∈[0,8]上的最小值,从而问题转化为利用单调性求函数f(x)=
在x∈[0,8]上的最小值,从而问题转化为利用单调性求函数f(x)=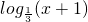 最小值问题,求得m的范围;(2)由(1)得命题p的等价命题,再求命题q的等价命题,根据p且q为假,p或q为真,利用真值表可推得p与q有且只有一个为真,分别解不等式组即可得m的取值范围.
最小值问题,求得m的范围;(2)由(1)得命题p的等价命题,再求命题q的等价命题,根据p且q为假,p或q为真,利用真值表可推得p与q有且只有一个为真,分别解不等式组即可得m的取值范围.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com