设
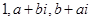
是一等比数列的连续三项,则a,b的值为( )
解:因为设
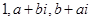
是一等比数列的连续三项,因此有
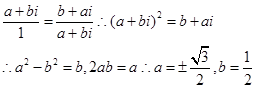
选C
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
在等比数列
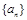
中,
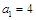
,公比为q,前n项和为
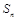
,若数列
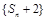
也是等比数列,则q等于
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数f(x)=log
2x,正项等比数列{b
n}的公比为2,若f(b
12.b
14…
.b
20)=4.则2
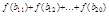
=
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知{a
n}为递增的等比数列,且{a
1,a
3,a
5}
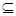
{-10,-6,-2,0,1,3,4,16}.
(1)求数列{a
n}的通项公式;
(2)是否存在等差数列{b
n},使得a
1b
n+a
2b
n-1+a
3b
n-2+…+a
nb
1=2
n+1-n-2对一切n∈N
*都成立?若存在,求出b
n;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设等比数列
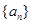
共有
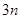
项,它的前
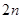
项的和为100,后
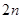
项之和为200,则该等比数列中间
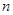
项的和等于
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
.在等比数列
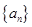
中,
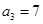
,前3项之和
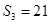
,则公比
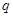
的值为 ( )
查看答案和解析>>

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案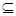 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.