练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当x＞0时，若函数f（x）=（3a-2）x的值总大于1，则实数a的取值范围是（　　）
    A、（
    2
    3
    ，1）
    B、（-∞，1）
    C、（1，+∞）
    D、（0，
    2
    3
    ）
    考点：指数函数的图像与性质
    专题：函数的性质及应用
    分析：根据已知已知条件能够判断出原指数函数为增函数，所以底数大于1，这样即可求出a的范围．
    解答：解：x＞0时，（3a-2）x＞1=（3a-2）0；
    ∴该指数函数应为增函数；
    ∴3a-2＞1；
    ∴a＞1，
    ∴实数a的范围为：（1，+∞）．
    故答案为：（1，+∞）．
    点评：考查指数函数的单调性，指数函数的单调性和底数的关系．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

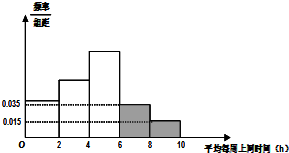    为了解高中生平均每周上网玩微信，刷微博，打游戏享受智能手机带来的娱乐生活体验，从高三年级学生中抽取部分同学进行调查，将所得的数据整理如下，画出频率分布直方图（如图），其中频率分布直方图从左至右前3个小组的频率之比为1：3：5，第二组的频数为150，则被调查的人数应为（　　）
    A、600B、400
    C、700D、500

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    现有如下错误推理：“复数是实数，i是复数，所以i是实数”．其错误的原因是（　　）
    A、使用了归纳推理
    B、使用了类比推理
    C、使用了“三段论”，但大前提错误
    D、使用了“三段论”，但推理形式错误

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点A（1，1），B（-1，
    		3
    ），直线l过原点，且与线段AB有交点，则直线l的斜率的取值范围为（　　）
    A、[-
    		3
    ，1]
    B、[1，+∞）
    C、（-∞，-
    		3
    ）
    D、（-∞，-
    		3
    ]∪[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x3+ax2+bx+c，其0＜f（-1）=f（-2）=f（-3）≤3，则（　　）
    A、c≤3B、3＜c≤6
    C、6＜c≤9D、c＞9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数y=（
    1
    2
    ）|x|在[a，b]（b＞a）上的值域为[
    1
    4
    ，1]，则b-a的最大值为（　　）
    A、6B、5C、4D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知变量x与y正相关，且由观测数据算得样本平均数
    .
    x
    =3，
    .
    y
    =3.5，则由该观测数据算得的线性回归方程可能是（　　）
    A、
    y
    =0.4x+2.3
    B、
    y
    =2x-2.4
    C、
    y
    =-2x+9.5
    D、
    y
    =-0.3x+4.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

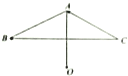    如图，已知O是△ABC所在平面内一点，满足
    AB
    +
    AC
    =
    AO
    ．且|
    OA
    |=|
    OB
    |=|
    OC
    |=|
    AB
    |=2，则
    CA
    在
    CB
    方向上的投影为（　　）
    A、1
    B、2
    C、
    		3
    D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设公比q=
    1
    2
    的等比数列{an}的前n项和为Sn，则
    S4
    a3
    =（　　）
    A、
    15
    2
    B、
    15
    4
    C、
    7
    2
    D、
    7
    4

    查看答案和解析>>

    同步练习册答案