
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
【答案】解:(Ⅰ)已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,整理得:2cosCsin(A+B)=sinC,
∵sinC≠0,sin(A+B)=sinC
∴cosC= ![]() ,
,
又0<C<π,
∴C= ![]() ;
;
(Ⅱ)由余弦定理得7=a2+b2﹣2ab ![]() ,
,
∴(a+b)2﹣3ab=7,
∵S= ![]() absinC=
absinC= ![]() ab=
ab= ![]() ,
,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周长为5+ ![]()
【解析】(Ⅰ)已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,根据sinC不为0求出cosC的值,即可确定出出C的度数;(2)利用余弦定理列出关系式,利用三角形面积公式列出关系式,求出a+b的值,即可求△ABC的周长.


科目:高中数学 来源: 题型:
【题目】下列四组函数,表示同一函数的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=x,g(x)= ![]()
C.f(x)=lnx2 , g(x)=2lnx
D.f(x)=logaax(a>0,a≠1),g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数,表示同一函数的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=x,g(x)= ![]()
C.f(x)=lnx2 , g(x)=2lnx
D.f(x)=logaax(a>0,a≠1),g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxcos![]() -
-![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求f(x)的最小正周期;
(2)若关于x的方程![]() 在x∈
在x∈![]() 上有两个不同的实根,求实数a的取值范围.
上有两个不同的实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是 .
①任取x>0,均有3x>2x;
②当a>0,且a≠1时,有a3>a2;
③y=( ![]() )﹣x是减函数;
)﹣x是减函数;
④函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
⑤若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
⑥y=x2﹣2|x|﹣3的递增区间为[1,+∞).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为矩形,PA⊥平面ABCD,PA=AB=2,AD=1,点M为PC中点,过A、M的平面α与此四棱锥的面相交,交线围成一个四边形,且平面α⊥平面PBC. 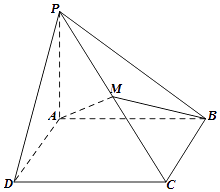
(1)在图中画出这个四边形(不必说出画法和理由);
(2)求平面α与平面ABM所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出的以下四个问题中,不需要用条件语句来描述其算法是( )
A.输入一个实数x,求它的绝对值
B.求面积为6的正方形的周长
C.求三个数a、b、c中的最大数
D.求函数f(x)= ![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 满足:
满足: ![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),证明:直线
不重合),证明:直线![]() 恒过定点,并求该定点的坐标.
恒过定点,并求该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com