Question

9．在△ABC中，AD是BC边上中线，下列错误的是（　　）

• A． $\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AD}$
• B． $\overrightarrow{AD}$+$\overrightarrow{DC}$=$\overrightarrow{AC}$
• C． $\overrightarrow{CA}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$
• D． $\overrightarrow{DB}$+$\overrightarrow{AD}$=$\overrightarrow{AB}$

Answer 1

分析 可根据向量加法的几何意义便可得出C错误，而对于D的判断，可根据向量数乘的几何意义，向量加法的平行四边形法，以及向量数乘运算便可判断出D正确．

解答 解：如图，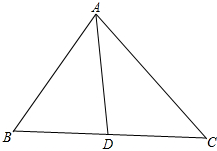

根据向量加法、减法的几何意义得：$\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$，$\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$，$\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{CD}≠\overrightarrow{DC}$；
$\overrightarrow{DB}+\overrightarrow{AD}=\frac{1}{2}\overrightarrow{CB}+\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$=$\frac{1}{2}（\overrightarrow{AB}-\overrightarrow{AC}）+\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）=\overrightarrow{AB}$；
∴C错误．
故选：C．

点评 考查向量加法、减法，及数乘的几何意义，向量加法的平行四边形法则，以及向量的数乘运算．