
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16 B.-16
C.a2-2a-16 D.a2+2a-16
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知i为虚数单位,复数z=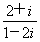 ,则|z|+
,则|z|+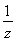 =( )
=( )
A.i B.1-I C.1+i D.-i
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:解答题
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:解答题
已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:选择题
设函数f(x)= 若f(a)+f(-1)=2,则a=( )
若f(a)+f(-1)=2,则a=( )
A.-3 B.±3
C.-1 D.±1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:选择题
对于非空实数集A,记A*={y|?x∈A,y≥x}.设非空实数集合M、P满足:M⊆P,且若x>1,则x∉P.现给出以下命题:
①对于任意给定符合题设条件的集合M、P,必有P*⊆M*;
②对于任意给定符合题设条件的集合M、P,必有M*∩P≠∅;
③对于任意给定符合题设条件的集合M、P,必有M∩P*=∅;
④对于任意给定符合题设条件的集合M、P,必存在常数a,使得对任意的b∈M*,恒有a+b∈P*.其中正确的命题是( )
A.①③ B.③④
C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则 的值为________.
的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题五练习卷(解析版) 题型:解答题
)如图所示,在三棱锥P-ABC中,AB=BC= ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=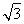 .
.

(1)证明:△PBC为直角三角形;
(2)求直线AP与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com